1751 - Maximum Number of Events That Can Be Attended II (Hard)
Problem Link
https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended-ii/
Problem Statement
You are given an array of events where events[i] = [startDayi, endDayi, valuei]. The ith event starts at startDayi and ends at endDayi, and if you attend this event, you will receive a value of valuei. You are also given an integer k which represents the maximum number of events you can attend.
You can only attend one event at a time. If you choose to attend an event, you must attend the entire event. Note that the end day is inclusive: that is, you cannot attend two events where one of them starts and the other ends on the same day.
Return the maximum sum of values that you can receive by attending events.
Example 1:
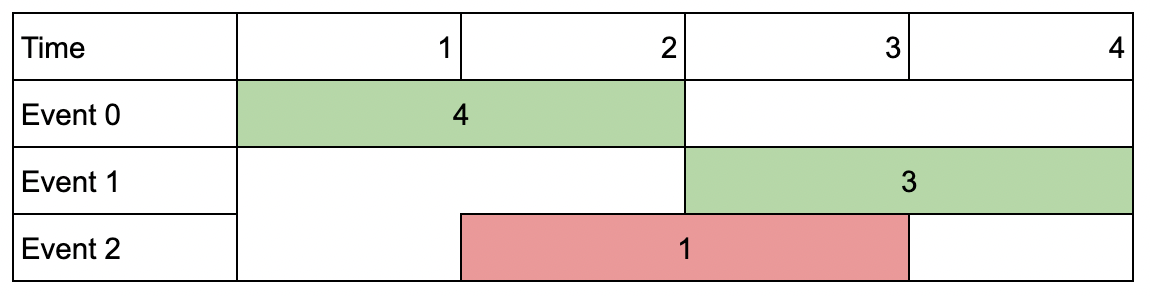
Input: events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
Output: 7
Explanation: Choose the green events, 0 and 1 (0-indexed) for a total value of 4 + 3 = 7.
Example 2:
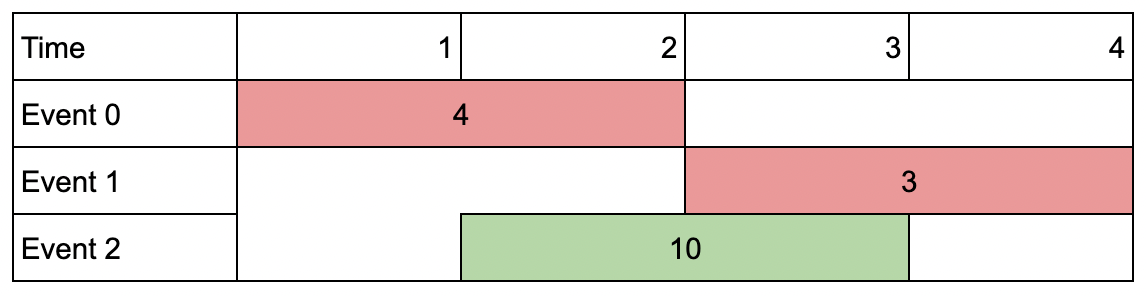
Input: events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
Output: 10
Explanation: Choose event 2 for a total value of 10.
Notice that you cannot attend any other event as they overlap, and that you do not have to attend k events.
Example 3:
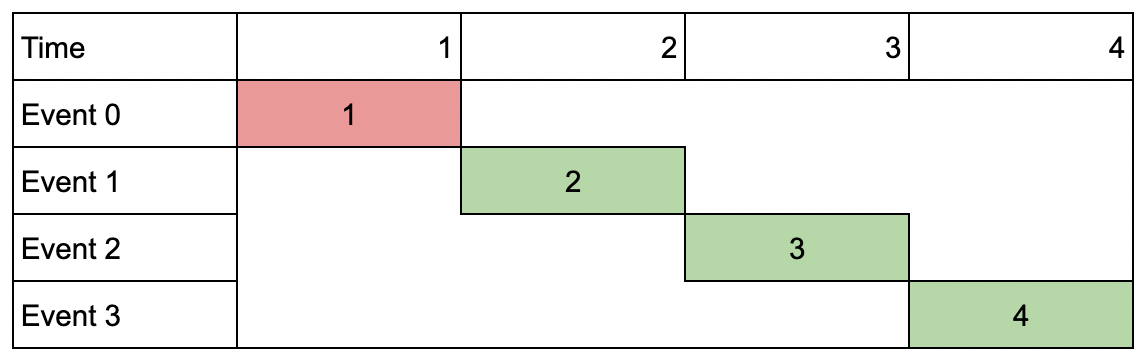
Input: events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
Output: 9
Explanation: Although the events do not overlap, you can only attend 3 events. Pick the highest valued three.
Constraints:
1 <= k <= events.length1 <= k * events.length <= 10^61 <= startDayi <= endDayi <= 10^91 <= valuei <= 10^6
Approach 1: Dynamic Programming
class Solution {
public:
int maxValue(vector<vector<int>>& events, int k) {
int n = events.size();
// sort by start time
sort(events.begin(), events.end());
// dp[i][j] means the max value we could get
// when we are at event i with k events left to join
vector<vector<int>> dp(n, vector<int>(k + 1, -1));
function<int(int,int,int)> dfs = [&](int idx, int k, int end) {
// reached all events or attended all k events
if (idx == n || k == 0) return 0;
// current start time <= previous end time
// cannot attend -> move to the next one
if (events[idx][0] <= end) return dfs(idx + 1, k, end);
// calculated before - return it immediately
if (dp[idx][k] != -1) return dp[idx][k];
// so we only have two choices left, we either
return dp[idx][k] = max(
// choice 1: attend this event
// and search for the next events starting from this end time
events[idx][2] + dfs(idx + 1, k - 1, events[idx][1]),
// choice 2: skip this event - search for the next one
dfs(idx + 1, k, end)
);
};
return dfs(0, k, 0);
}
};