0329 - Longest Increasing Path in a Matrix (Hard)

Problem Link

https://leetcode.com/problems/longest-increasing-path-in-a-matrix/

Problem Statement

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

Example 1:

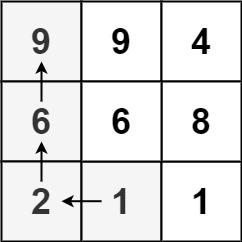
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

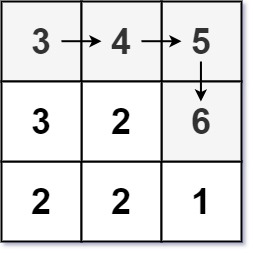
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Example 3:

Input: matrix = [[1]]
Output: 1

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 2^31 - 1

Approach 1: Dynamic Programming - Memoization

We can very easily run a DFS on each cell, calculating the path length for each traversal, and tracking a global longest path. Obviously, we would end up doing a lot of the same work though, so we can store it in a hash map, to reuse the work for later.

Our DFS function will need to track current position in the matrix, as well as the value of the cell we are coming from, and our cache will need to store the length of the path to traverse to cell $(r,c)$ where $r$ is the row index, and $c$ is the column index.

Time Complexity: $O(m*n)$, where $m$ is $matrix.length$ and $n$ in $matrix[i].length$. We are going to have to traverse each cell in the matrix, but we only have to do so once as we can reuse work from previous traversals of each cell.

Space Complexity: $O(m*n)$. Our hash map storing our reused work will take up to $m*n$ space as we may store up to $m*n$ key, value pairs inside.

Python

Written by @ColeB2

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        # Store constants, size of the matrix and directions of traversal
        ROWS, COLS = len(matrix), len(matrix[0])
        DIRS = ((1,0), (0,1), (-1,0), (0,-1))
        # initialize the longest path, and our memoization cache.
        self.longest_path = 1
        # cache: key -> (row, col) value: integer, path length to cell.
        cache = {}
        # DFS, track current r, c coordinate, and value previous cell
        # we came from.
        def dfs(r, c, prev_cell):
            # base case, if we cacluated path length of the longest path
            # to current cell before:
            if (r,c) in cache:
                # return that path length.
                return cache[(r,c)]
            
            # initialize path length to 1, as a 1 cell path starts as 1.
            path = 1
            # traverse our 4 directions
            for dr, dc in DIRS:
                new_r, new_c = r + dr, c + dc
                # check if we are inbounds, and that the new cell
                # we are going to is greater than current cell.
                if (0 <= new_r < ROWS and
                    0 <= new_c < COLS and
                    matrix[new_r][new_c] > matrix[r][c]
                    ):
                    # if it is, update the path length with recursive
                    # call return value + 1.
                    path = max(path, 1 + dfs(new_r, new_c, matrix[r][c]))
                    # update the longest path when we find it.
                    self.longest_path = max(path, self.longest_path)
            # store the longest path we can create for (r,c)
            cache[(r,c)] = path
            return path

        # iterate our matrix
        for r in range(ROWS):
            for c in range(COLS):
                # call DFS on each cell. Initialize prev_cell value of 
                # inf as all other values will be below that.
                dfs(r, c, float('inf'))
        return self.longest_path

Approach 2: Topological Sort

We can create a directed graph, track the dependencies for each node in the graph, traverse it, and find the length of the longest path.

We would do this by tracking an adjacency list, which would be a hash map that maps each $(row, column)$ coordinate to any other cells (row, column) coordinate which is greater than it. Thus creating a directed graph which will only point to increasing values.

We must also track dependencies for each cell so that we can only start at the start points of these paths. We can put these cells with an $indegrees$ of $0$ into a queue, then use that queue to traverse all the paths, updating the queue any time the $indegrees$ of another cell reaches $0$.

Time Complexity: $O(m*n)$ where $m$ is $matrix.length$ and $n$ in $matrix[i].length$. We are going to visit each cell once during the topological sort and check each neighbour.

Space Complexity: $O(m*n)$ as well, to track our $indegrees$ array and our $queue$, as well as our $adjacency list$.

Python

Written by @ColeB2

class Solution:
    def longestIncreasingPath(self, matrix: List[List[int]]) -> int:
        # store our constants.
        ROWS, COLS = len(matrix), len(matrix[0])
        DIRS = ((1,0), (0,1), (-1,0), (0,-1))
        # initialze our adjacency list and indegrees
        # adj_list key: (row, col) value: (row,col) of cell we can
        # traverse to.
        adj_list = defaultdict(list)
        # indegrees[row][col] will represent a cell that has a value
        # that can travel to us.
        indegrees = [[0] * COLS for _ in range(ROWS)]
        # iterate matrix
        for r in range(ROWS):
            for c in range(COLS):
                # for each cell in matrix, iterate 4 adjacent cells
                for dr, dc in DIRS:
                    new_r, new_c = r + dr, c + dc
                    # check new cell is inbounds and the value of the
                    # new cell is increasing.
                    if (0 <= new_r < ROWS and
                        0 <= new_c < COLS and
                        matrix[new_r][new_c] > matrix[r][c]
                        ):
                        # add new cell to our adjacency list. Current
                        # cell can traverse to the new cell.
                        adj_list[(r,c)].append((new_r, new_c))
                        # update indegrees. Found 1 cell that points to 
                        # our new cell.
                        indegrees[new_r][new_c] += 1
        # find all cells that have indegrees of 0. Ie cells that have
        # no dependencies, or other cells point to them. Our start points.
        q = deque()
        for r in range(ROWS):
            for c in range(COLS):
                # indegrees 0, add to the queue.
                if indegrees[r][c] == 0:
                    # queue (row, col, path_length)
                    q.append((r,c,1))
        # track global longest path
        longest_path = 1
        while q:
            # pop position r, c and length of current path
            r, c, path = q.popleft()
            #update longest path length
            longest_path = max(longest_path, path)
            # traverse to all cells from current path that are increasing.
            for row, col in adj_list[(r,c)]:
                # decremenet the indegrees of these new cells as we
                # we traverse to them
                indegrees[row][col] -= 1
                # indegrees reaches 0, we can add it to our queue.
                if indegrees[row][col] == 0:
                    q.append((row, col, path + 1))
        return longest_path