0543 - Diameter of Binary Tree (Easy)
Problem Link
https://leetcode.com/problems/diameter-of-binary-tree/
Problem Statement
Given the root of a binary tree, return the length of the diameter of the tree.
The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
The length of a path between two nodes is represented by the number of edges between them.
Example 1:
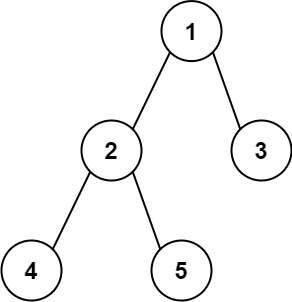
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].
Example 2:
Input: root = [1,2]
Output: 1
Constraints:
- The number of nodes in the tree is in the range
[1, 10^4]. -100 <= Node.val <= 100
Approach 1: Recursive Depth-First Search
Like most tree problems, they can often be solved using recursion. Thinking about the brute force, of solving this from the top down, that is calculating the height of the left and right sub-tree, would obviously leave us with a lot of repeated work to cacluate that for each node. So bottoms-up, which is often how our recursion will solve it sounds like a much easier plan.
Like any recursive algorithm we must first think of our base case. For a tree that would be, what does a null node return? We can return 0 for that since a null node would have no edges, and a parent pointing to a null node doesn't have a legitimate edge pointing to it. So it's diameter would be 0.
So what next? Well we know if we aren't a null node, that to get the diameter, we need the length of the longest path of both the left and right sub-trees to solve it for the current node. This is where the recursion comes in, so we can recursively call our algorithm on both the left and right sub-trees to help us get the diameter of the current node.
So now we have a diameter, what do we do with it? Well, we probably need a global diameter to check it against, since the max diameter doesn't necessarily run through the root, we will need to check it against what the global is. This tells us we probably need to use a helper function to calculate everything, and then update a global diameter once we find the diameter for each node.
Finally we can return up the length of the longest sub-tree, left or right, adding 1 to it to account for the path back to the parent so that the parent can calulate it's diameter.
Time Complexity: as we are going to have to traverse each node in the tree, and can't skip any nodes.
Space Complexity: , as with most recursive DFS, we are only going to have the current path we are taking inside the call stack, which will scale with the height of the tree.
- Python
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
# set global diameter, our return value. Initialize as 0.
self.diameter = 0
# helper function - recursive Depth-First Search.
def helper(node):
# Base case, reaches null node, return height of 0.
if not node:
return 0
# recursively check left and right children nodes to get the max
# height of each sub-tree.
l = helper(node.left)
r = helper(node.right)
# diamater for the current node will be solved by calculating the
# max height of each sub-tree and adding them together.
# update global diameter, with current nodes diameter.
self.diameter = max(self.diameter, l + r)
# Now we don't want to pass the diameter up, we just want to pass the
# height of the longest sub-tree up. So return 1 + max height of either
# the left or right sub-tree.
return 1 + max(l, r)
# call helper function - helper function will update our global
# diameter so no need for us to assign a value to anything.
helper(root)
# return diameter we calcuated.
return self.diameter