1168 - Optimize Water Distribution in a Village (Hard)

Problem Link

https://leetcode.com/problems/optimize-water-distribution-in-a-village/

Problem Statement

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes where each pipes[j] = [house1j, house2j, costj] represents the cost to connect house1j and house2j together using a pipe. Connections are bidirectional, and there could be multiple valid connections between the same two houses with different costs.

Return the minimum total cost to supply water to all houses.

Example 1:

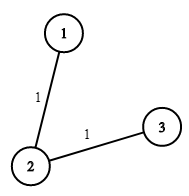
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

Example 2:

Input: n = 2, wells = [1,1], pipes = [[1,2,1],[1,2,2]]
Output: 2
Explanation: We can supply water with cost two using one of the three options:
Option 1:
  - Build a well inside house 1 with cost 1.
  - Build a well inside house 2 with cost 1.
The total cost will be 2.
Option 2:
  - Build a well inside house 1 with cost 1.
  - Connect house 2 with house 1 with cost 1.
The total cost will be 2.
Option 3:
  - Build a well inside house 2 with cost 1.
  - Connect house 1 with house 2 with cost 1.
The total cost will be 2.
Note that we can connect houses 1 and 2 with cost 1 or with cost 2 but we will always choose the cheapest option. 

Constraints:

• 2 <= n <= 10^4
• wells.length == n
• 0 <= wells[i] <= 105
• 1 <= pipes.length <= 10^4
• pipes[j].length == 3
• 1 <= house1j, house2j <= n
• 0 <= costj <= 105
• house1j != house2j

Approach 1: Kruskal's Algorithm

If we add a new house, says house 0, and connect it to each houses with weight $wells[i]$. Then this problem is actually same as finding Minimum Spanning Tree. Hence, we can use Kruskal's Algorithm with DSU to solve it.

In order to get the MST, we sort the edges based on the weights in an increasing order. Then we iterate them one by one, and greedily pick edges which does not result in cycle with the previous edges.

Written by @wingkwong

class dsu {
 public:
  vector<int> root, rank;
  int n;
  int cnt;

  dsu(int _n) : n(_n) {
    root.resize(n);
    rank.resize(n);
    for(int i = 0; i < n; i++) {
        root[i] = i;
        rank[i] = 1;
    }
    cnt = n;
  }

  inline int getCount() { return cnt; }

  inline int get(int x) { return (x == root[x] ? x : (root[x] = get(root[x]))); }

  inline bool unite(int x, int y) {
    x = get(x);
    y = get(y);
    if (x != y) {
        if (rank[x] > rank[y]) {
            root[y] = x;
        } else if (rank[x] < rank[y]) {
            root[x] = y;
        } else {
            root[y] = x;
            rank[x] += 1;
        }
        cnt--;
      return true;
    }
    return false;
  }
};

class Solution {
public:
    int minCostToSupplyWater(int n, vector<int>& wells, vector<vector<int>>& pipes) {
        vector<array<int, 3>> edges;
        for (int i = 0; i < wells.size(); i++) edges.push_back({wells[i], 0, i + 1});
        for (auto x : pipes) edges.push_back({x[2], x[0], x[1]});
        sort(edges.begin(), edges.end());
        dsu d(n + 1);
        int ans = 0;
        for (auto x : edges) {
            if (d.unite(x[1], x[2])) {
                ans += x[0];
            }
        }
        return ans;
    }
};