Skip to main content

1259 - Handshakes That Don't Cross (Hard)

https://leetcode.com/problems/handshakes-that-dont-cross/

Problem Statement​

You are given an even number of people numPeople that stand around a circle and each person shakes hands with someone else so that there are numPeople / 2 handshakes total.

Return the number of ways these handshakes could occur such that none of the handshakes cross.

Since the answer could be very large, return it modulo 109 + 7.

Example 1:

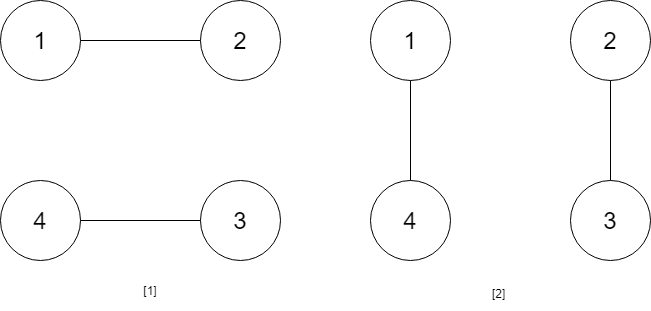
Input: numPeople = 4
Output: 2
Explanation: There are two ways to do it, the first way is [(1,2),(3,4)] and the second one is [(2,3),(4,1)].

Example 2:

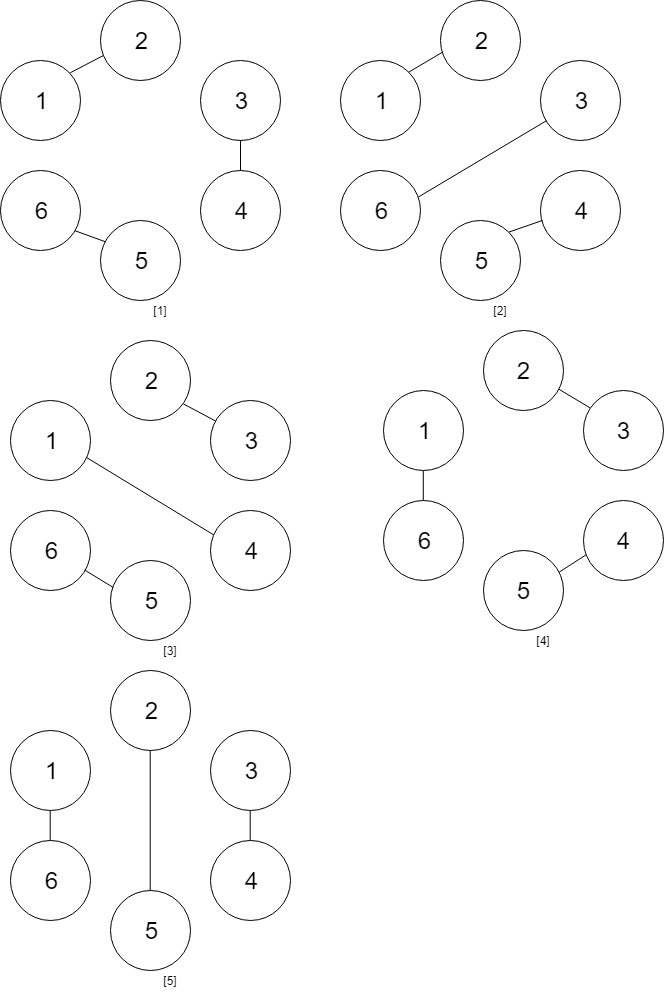
Input: numPeople = 6
Output: 5

Constraints:

  • 2 <= numPeople <= 1000
  • numPeople is even.

Approach 1: Dynamic Programming​

Person 1 can shake hand with person with even number but not with odd number because every time we need to divide the group into two sets. For example, if person 1 shakes hand with person 2, then there is an empty set and a set of people with numbers from 3 to n. If person 1 shakes hand with person 4, then the first set is person 2 + person 3 and the second set is from 5 to n. At the end, we would have a set from person 2 to n - 1 and an empty set.

In general, let dp[i]dp[i] be the number of ways these handshakes could occur such that none of the handshakes cross of for ii people. If person ii shakes hand with person jj, then we could divide into two sets - one from 2 to j - 1 and another one from j - 1 to i. The product of them would be the contribution to dp[i]dp[i].

Written by @wingkwong
class Solution {
public:
    int numberOfWays(int n) {
        int M = 1e9 + 7;
        vector<long long> dp(n + 1, 0);
        dp[0] = 1;
        for (int i = 2; i <= n; i += 2) {
            for (int j = 2; j <= i; j += 2) {
                // two sets : 
                // 1. [2 .. j - 1] = j - 1 - 2 + 1 = j - 2
                // 2. [j + 1 .. i] = i - (j + 1) + 1 = i - j
                dp[i] = (dp[i] + (dp[j - 2] * dp[i - j])) % M;
            }
        }
        return dp[n];
    }
};