1305 - All Elements in Two Binary Search Trees (Medium)

Problem Link

https://leetcode.com/problems/all-elements-in-two-binary-search-trees/

Problem Statement

Given two binary search trees root1 and root2, return a list containing all the integers from both trees sorted in ascending order.

Example 1:

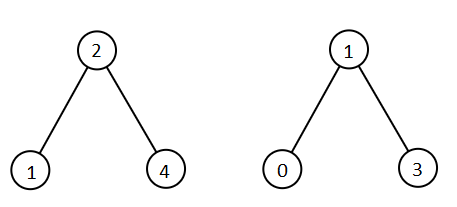
Input: root1 = [2,1,4], root2 = [1,0,3]
Output: [0,1,1,2,3,4]

Example 2:

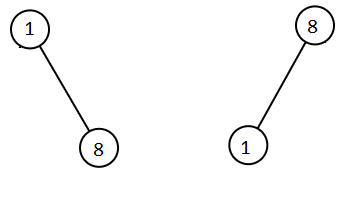
Input: root1 = [1,null,8], root2 = [8,1]
Output: [1,1,8,8]

Constraints:

• The number of nodes in each tree is in the range [0, 5000].
• -10^5 <= Node.val <= 10^5

Prerequisite

• Binary Tree

Approach 1: DFS Traversal and Sorting

In this problem, we can use either one to traverse all nodes and put them into a common array. We sort the array at the end.

Written by @wingkwong

class Solution {
public:
    vector<int> s;
    
    void dfs(TreeNode* node) {
        if (node == NULL) return;
        dfs(node->left);
        s.push_back(node->val);
        dfs(node->right);
    }
    
    vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
        dfs(root1);
        dfs(root2);
        sort(s.begin(), s.end());
        return s;
    }
};

However, we can see the in-order traversal is faster than the other two. This is because the array is already sorted after the traversal for binary tree. In example 1, after the traversal, we will have [1, 2, 4] and [0, 1, 3].

Traversal	Runtime	Memory	Language
Pre-order	309 ms	85.4 MB	cpp
In-order	132 ms	85.3 MB	cpp
Post-order	211 ms	85.4 MB	cpp

Approach 2: In-order Traversal + Merging

As we know In-order traversal will make the array sorted, the remaining problem is same as "merging two sorted arrays into one".

Written by @wingkwong

class Solution {
public:
    void inorder(TreeNode* node, vector<int>& res) {
        if (node == NULL) return;
        inorder(node->left, res);
        res.push_back(node->val);
        inorder(node->right, res);
    }
    
    vector<int> merge(vector<int>& a, vector<int>& b) {
        vector<int> res;
        int n = (int) a.size(), m = (int) b.size();
        int i = 0, j = 0;
        while (i < n && j < m) {
            if (a[i] < b[j]) res.push_back(a[i++]);
            else res.push_back(b[j++]);
        }
        while (i < n) res.push_back(a[i++]);
        while (j < m) res.push_back(b[j++]);
        return res;
    }
    
    vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
        vector<int> a, b;
        inorder(root1, a); inorder(root2, b);
        return merge(a, b);
    }
};