1334 - Find the City With the Smallest Number of Neighbors at a Threshold Distance (Medium)

Problem Link

https://leetcode.com/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/

Problem Statement

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

Example 1:

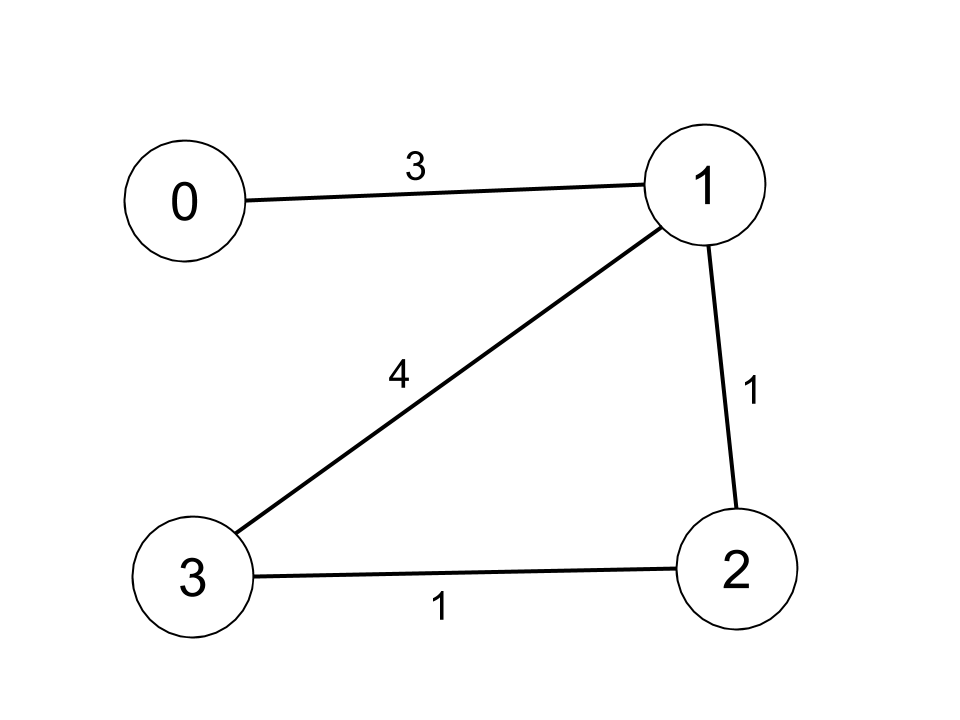
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

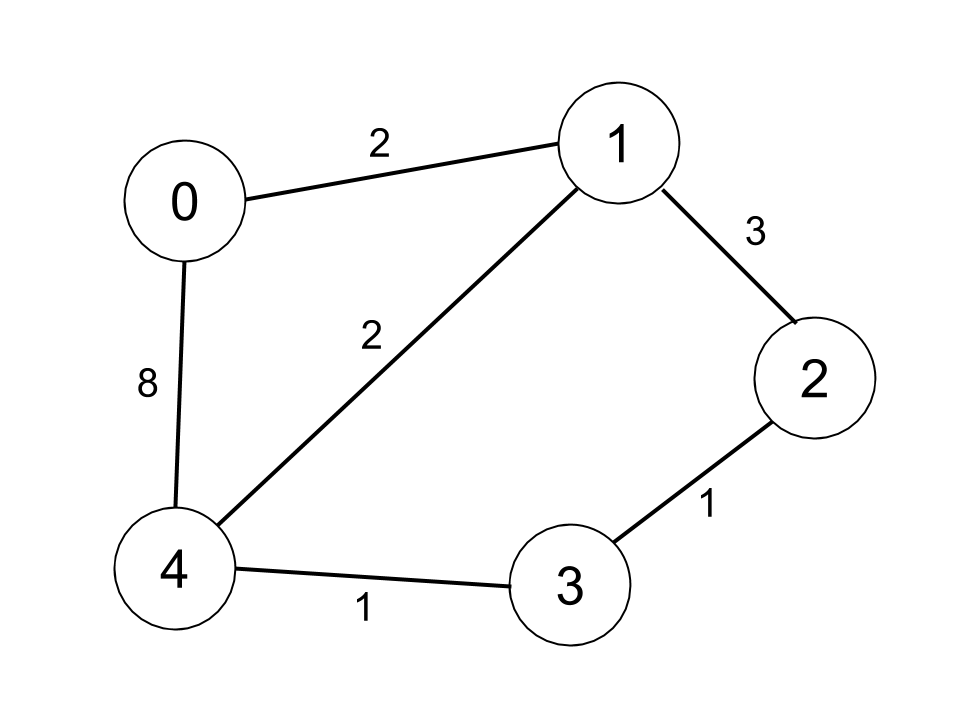
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
The city 0 has 1 neighboring city at a distanceThreshold = 2. 

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• All pairs (fromi, toi) are distinct.

Approach 1: Floyd Warshall Algorithm

Since $n$ is small, we can use Floyd Warshall Algorithm to calculate the distances between each node. Let $dist[i][j]$ be the distance beween node $i$ and node $j$. Once we know all the distances, we can iterate each node $i$, and check each node $j$ to see if the distance is less than / equal to $distanceThreshold$. If so, we count it and check the minimal value.

Written by @wingkwong

class Solution {
public:
    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        // ----------- Floyd Warshall ---------------/
        vector<vector<int>> dist(n, vector<int>(n, 1e9));
        for (int i = 0; i < n; i++) dist[i][i] = 0;
        for (auto x : edges) {
            dist[x[0]][x[1]] = x[2];
            dist[x[1]][x[0]] = x[2];
        }
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
                }
            }
        }
        // ----------- Floyd Warshall ---------------/
        int ans = 0, mi = n;
        // iterate each node
        for (int i = 0; i < n; i++) {
            // check each node to see 
            // if the distance is at most distanceThreshold
            int cnt = 0;
            for (int j = 0; j < n; j++) {
                cnt += dist[i][j] <= distanceThreshold;
            }
            // use <= instead of <  
            // because we need to return the city with the greatest number
            if (cnt <= mi) {
                mi = cnt;
                ans = i;
            }
        }
        return ans;
    }
};

Approach 2: Dijkstra's Algorithm

We can perform Dijkstra's algorithm on each node to calculate the distances between that node and other nodes. Iterate them and check if the distance is at most $distanceThreshold$. If so, update the minimum counter and the answer.

Written by @wingkwong

class Solution {
public:
    template<typename T_pair, typename T_vector>
        void dijkstra(T_pair &g, T_vector &dist, int start) {
          priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
          dist[start] = 0;
          pq.push({start, 0});
          while (!pq.empty()) {
            auto [u_node, u_cost] = pq.top(); pq.pop();
            if (u_cost > dist[u_node]) continue;
            for (auto [v_node, v_cost] : g[u_node]) {
              if (dist[v_node] > dist[u_node] + v_cost) {
                dist[v_node] = dist[u_node] + v_cost;
                pq.push({v_node, dist[v_node]});
              }
            }
          }
        }

    int findTheCity(int n, vector<vector<int>>& edges, int distanceThreshold) {
        int ans = 0, mi_cnt = 1e9;
        vector<vector<pair<int, int>>> g(n);
        for (auto x : edges) {
            // x[0] -> x[1] with cost x[2]
            g[x[0]].push_back({x[1], x[2]});
            // x[1] -> x[0] with cost x[2]
            g[x[1]].push_back({x[0], x[2]});
        }
        // iterate each node
        for (int i = 0; i < n; i++) {
            // perform dijkstra
            vector<int> dist(n, 1e9);
            dijkstra(g, dist, i);
            int cnt = 0;
            // iterate each node
            for (int j = 0; j < n; j++) {
                // bypass the same node
                if (i == j) continue;
                // if reachable, count if the distance is at most distanceThreshold
                cnt += dist[j] <= distanceThreshold;
            }
            // update mi_cnt and ans
            if (cnt <= mi_cnt) mi_cnt = cnt, ans = i;
        }
        return ans;
    }
};