Skip to main content

1572 - Matrix Diagonal Sum (Easy)

https://leetcode.com/problems/matrix-diagonal-sum/

Problem Statement​

Given a square matrix mat, return the sum of the matrix diagonals.

Only include the sum of all the elements on the primary diagonal and all the elements on the secondary diagonal that are not part of the primary diagonal.

Example 1:

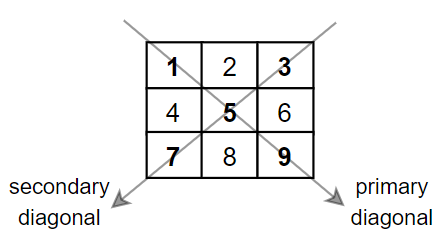
Input: mat = [[1,2,3],
              [4,5,6],
              [7,8,9]]
Output: 25
Explanation: Diagonals sum: 1 + 5 + 9 + 3 + 7 = 25
Notice that element mat[1][1] = 5 is counted only once.

Example 2:

Input: mat = [[1,1,1,1],
              [1,1,1,1],
              [1,1,1,1],
              [1,1,1,1]]
Output: 8

Example 3:

Input: mat = [[5]]
Output: 5

Constraints:

  • n == mat.length == mat[i].length
  • 1 <= n <= 100
  • 1 <= mat[i][j] <= 100

Approach 1: Iteration​

We have to first iterate the primary diagonal first. In the primary diagonal, the row number equals to the column number, so it is pretty straightforward to get the numbers on the primary diagonal. On the secondary diagonal, the column number decreases as row number increases, and you should be able to obtain the relation col = len(mat) - row - 1. We also have to be mindful to avoid computing the element at mat[len(mat)//2][len(mat)//2] twice, so we add a conditional check to skip if it exists. Note that this does not always exist (if the dimension of the matrix is two even numbers)

Written by @heiheihang
def diagonalSum(self, mat: List[List[int]]) -> int:
        
        #initialize result
        result = 0
        
        #add all values in primary diagonal
        for row in range(len(mat)):
            #col = row in primary diagonal
            col = row 
            
            #add the value to result
            result += mat[row][col]
        
        #add all values in secondary diagonal
        for row in range(len(mat)):
            
            #col is the the opposite end of row in secondary diagonal
            col = len(mat) - row - 1
            
            #to avoid adding the center number twice, we skip if row == col
            if(row == col):
                continue
                
            #add the value to result
            result += mat[row][col]
        
        #return result
        return result