1547 - Minimum Cost to Cut a Stick (Hard)

Problem Link

https://leetcode.com/problems/minimum-cost-to-cut-a-stick/

Problem Statement

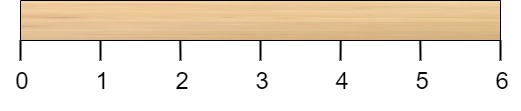
Given a wooden stick of length n units. The stick is labelled from 0 to n. For example, a stick of length 6 is labelled as follows:

Given an integer array cuts where cuts[i] denotes a position you should perform a cut at.

You should perform the cuts in order, you can change the order of the cuts as you wish.

The cost of one cut is the length of the stick to be cut, the total cost is the sum of costs of all cuts. When you cut a stick, it will be split into two smaller sticks (i.e. the sum of their lengths is the length of the stick before the cut). Please refer to the first example for a better explanation.

Return the minimum total cost of the cuts.

Example 1:

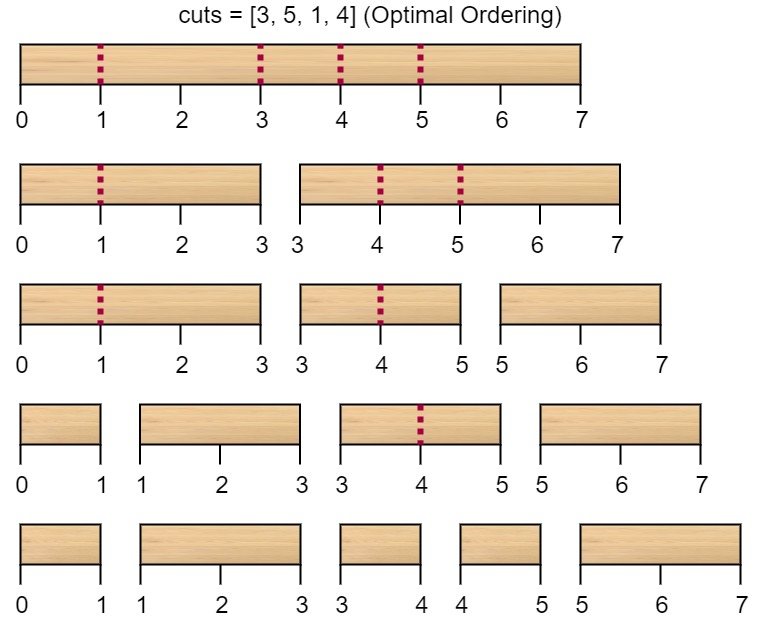
Input: n = 7, cuts = [1,3,4,5]
Output: 16
Explanation: Using cuts order = [1, 3, 4, 5] as in the input leads to the following scenario:

The first cut is done to a rod of length 7 so the cost is 7. The second cut is done to a rod of length 6 (i.e. the second part of the first cut), the third is done to a rod of length 4 and the last cut is to a rod of length 3. The total cost is 7 + 6 + 4 + 3 = 20.
Rearranging the cuts to be [3, 5, 1, 4] for example will lead to a scenario with total cost = 16 (as shown in the example photo 7 + 4 + 3 + 2 = 16).

Example 2:

Input: n = 9, cuts = [5,6,1,4,2]
Output: 22
Explanation: If you try the given cuts ordering the cost will be 25.
There are much ordering with total cost <= 25, for example, the order [4, 6, 5, 2, 1] has total cost = 22 which is the minimum possible.

Constraints:

• 2 <= n <= 10^6
• 1 <= cuts.length <= min(n - 1, 100)
• 1 <= cuts[i] <= n - 1
• All the integers in cuts array are distinct.

Approach 1: Dynamic Programming

Let $dp[i][j]$ be the minimum total cost between cut position $i$and $j$. First let's add $0$ and $n$ to the input for further calculation. Then we sort the input in ascending order. We can perform a dfs function $dfs(cuts, 0, (int) cuts.size() - 1)$ to get the answer.

Let's think of the base case first. Since the minimum length of a rod is $1$, we reach the destination when $j - i <= 1$ because we cannot make further cuts anymore. If $dp[i][j]$ has been calculated before, we can return it immediately.

Otherwise, we iterate each position$k$ and perform each possible cut. We know that the cost is the length of the rod to be cut, i.e. $cuts[j] - cuts[i]$. In example 1, the first cut costs 7. Since we have added $0$ and $n$to the input, so we have covered that. Once we cut at a certain point, the rod will be split into two parts. We perform the logic to calculate the costs for these two parts until we perform all the cuts.

Written by @wingkwong

class Solution {
public:
    // memoization
    int dp[105][105];
    int dfs(vector<int>& cuts, int i, int j) {
        // the smallest rod has length of 1
        if (j - i <= 1) return 0;
        // if the cost is calculated before, return immediately
        if (dp[i][j] != -1) return dp[i][j];
        // we initialise a large number since we are looking for the minimum number
        int ans = 1e9;
        //
        for (int k = i + 1; k < j; k++) {
            // if this rod is to be cut, the cost is the length, 
            // i.e. cuts[j] - cuts[i]
            // after the cut, it will be split into two parts
            // then we calculate the cost for left rod : dfs(cuts, i, k) 
            // and the cost for the right rod: dfs(cuts, k, j)
            ans = min(ans, cuts[j] - cuts[i] + dfs(cuts, i, k) + dfs(cuts, k, j));
        }
        // memoize the ans 
        return dp[i][j] = ans;
    }
    
    int minCost(int n, vector<int>& cuts) {
        cuts.push_back(0);
        cuts.push_back(n);
        sort(cuts.begin(), cuts.end());
        memset(dp, -1, sizeof(dp));
        return dfs(cuts, 0, (int) cuts.size() - 1);
    }
};