1692 - Count Ways to Distribute Candies (Hard)

Problem Link

https://leetcode.com/problems/count-ways-to-distribute-candies/

Problem Statement

There are n unique candies (labeled 1 through n) and k bags. You are asked to distribute all the candies into the bags such that every bag has at least one candy.

There can be multiple ways to distribute the candies. Two ways are considered different if the candies in one bag in the first way are not all in the same bag in the second way. The order of the bags and the order of the candies within each bag do not matter.

For example, (1), (2,3) and (2), (1,3) are considered different because candies 2 and 3 in the bag (2,3) in the first way are not in the same bag in the second way (they are split between the bags (2) and (1,3)). However, (1), (2,3) and (3,2), (1) are considered the same because the candies in each bag are all in the same bags in both ways.

Given two integers, n and k, return the number of different ways to distribute the candies. As the answer may be too large, return it modulo 109 + 7.

Example 1:

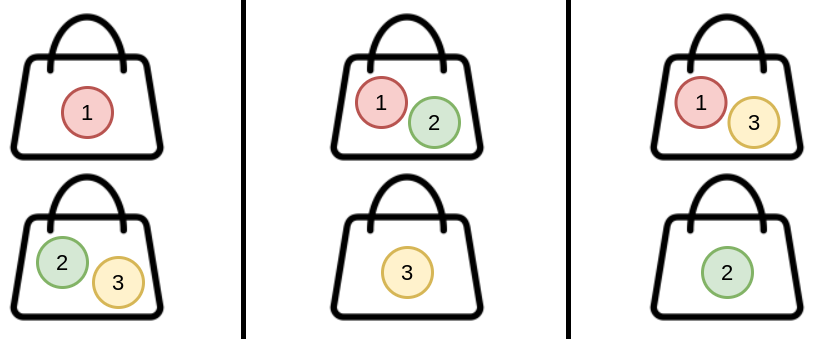
Input: n = 3, k = 2
Output: 3
Explanation: You can distribute 3 candies into 2 bags in 3 ways:
(1), (2,3)
(1,2), (3)
(1,3), (2)

Example 2:

Input: n = 4, k = 2
Output: 7
Explanation: You can distribute 4 candies into 2 bags in 7 ways:
(1), (2,3,4)
(1,2), (3,4)
(1,3), (2,4)
(1,4), (2,3)
(1,2,3), (4)
(1,2,4), (3)
(1,3,4), (2)

Example 3:

Input: n = 20, k = 5
Output: 206085257
Explanation: You can distribute 20 candies into 5 bags in 1881780996 ways. 1881780996 modulo 109 + 7 = 206085257.

Constraints:

• 1 <= k <= n <= 1000

Approach 1: Dynamic Programming

Let dp[k][n] be number of ways to distribute n candies into k bags.

If k > n, then dp[k][n] = 0 because each bag must have at least one ball which this condition cannot be satisfied.

If k == n, then dp[k][n] = 1 because obviously there is only one way to do it.

If k < n, we have two possible actions - either put n-th candy into any of the existing k bags or put it into a new bag. For example, if we have 3 balls and 3 bags, what we can do for 3 balls 2 bags case? We either put 2 balls into 2 bags and the third goes to any of the two bags, or we put two balls into 1 bag and put the third one into the other one. Therefore, we have the following formula.

$$dp[2 bags][3 balls] = dp[2 bags][2 balls] * 2 bags + dp[1 bag][2 balls]$$

To generalise, we have such transition.

$$dp[i][j] = dp[i][j - 1] * i + dp[i - 1][j - 1]$$

Written by @wingkwong

class Solution {
public:
    int M = 1e9 + 7;
    long long dfs(vector<vector<long long>>& dp, int n, int k) {
        if (n < k || k == 0) return 0;
        if (n == k) return 1;
        if (dp[n][k] != -1) return dp[n][k];
        return dp[n][k] = (dfs(dp, n - 1, k) * k + dfs(dp, n - 1, k - 1)) % M;
    }
    
    int waysToDistribute(int n, int k) {
        vector<vector<long long>> dp(n + 1, vector<long long>(k + 1, -1));
        return dfs(dp, n, k);
    }
};

Written by @wingkwong

class Solution {
public:
    int waysToDistribute(int n, int k) {
        int M = 1e9 + 7;
        // dp[k][n] : number of ways to distribute n candies into k bags
        vector<vector<long long>> dp(k + 1, vector<long long>(n + 1));
        for(int i = 0; i <= k; i++) dp[i][i] = 1;
        for(int i = 1; i <= k; i++) {
            for(int j = i + 1; j <= n; j++) {
                dp[i][j] = (i * dp[i][j - 1] + dp[i - 1][j - 1]) % M;
            }
        }
        return dp[k][n];
    }
};

Approach 2: Combinatorics

This problem is exactly asking Stirling number of the second kind (or Stirling partition number) which is the number of ways to partition a set of n objects into k non-empty subsets.

Stirling partition number can be calculated by using the following formula.

$$S(n,k)=\frac1{k!}\sum_{j=0}^k(-1)^j\binom{k}j(k-j)^n$$

Written by @wingkwong

class Solution:
    def waysToDistribute(self, n: int, k: int) -> int:
        return int(sum((-1) ** j * comb(k, j) * (k - j) ** n 
                    for j in range(k)) // factorial(k)  % (10 ** 9 + 7))