1631 - Path With Minimum Effort (Medium)

Problem Link

https://leetcode.com/problems/path-with-minimum-effort/

Problem Statement

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

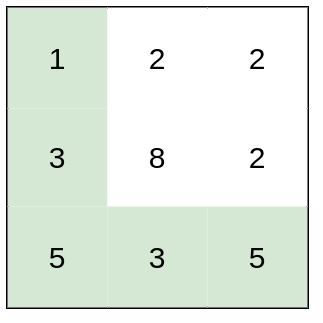
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

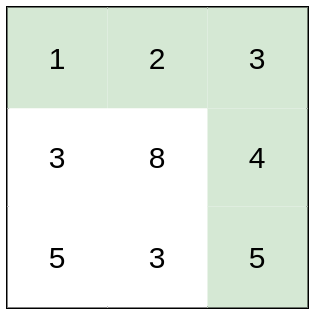
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

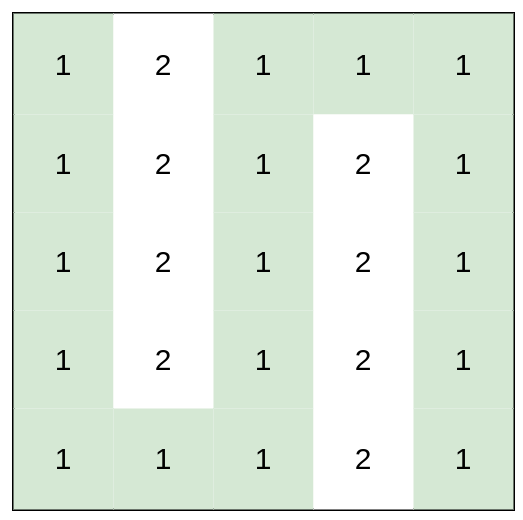
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort. 

Constraints:

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 10^6

Approach 1: DFS + Binary Search

Give the constraints, we know the absolute difference values would be between $[0, 1e6]$. Also looking for min max value gives a hint that we can use Binary Search to look for the possible absolute difference $k$, adn use DFS to walk the grid to see if the destination can be reached given $k$.

C++

Written by @wingkwong

class Solution {
public:
    int dirx[4] = { -1, 0, 0, 1 };
    int diry[4] = { 0, 1, -1, 0 };
    void dfs(vector<vector<int>>& heights, vector<vector<int>>& vis, int i, int j, int mid) {
        vis[i][j] = 1;
        for (int d = 0; d < 4; d++) {
            int x = i + dirx[d], y = j + diry[d];
            if (x < 0 || x >= heights.size() || y < 0 || y >= heights[0].size() || vis[x][y]) continue;
            // if it is out of the target mid, then skip
            if (abs(heights[i][j] - heights[x][y]) > mid) continue;
            dfs(heights, vis, x, y, mid);
        }
    }
    
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = (int) heights.size(), n = m ? (int) heights[0].size() : 0;
        // init possible range
        int l = 0, r = 1e6;
        while(l < r) {
            // get the middle one
            // for even number of elements, take the lower one
            int mid = l + (r - l) / 2;
            vector<vector<int>> vis(m, vector<int>(n, 0));
            // call dfs to check if the dist can be reached or not
            dfs(heights, vis, 0, 0, mid);
            // exclude mid
            if(!vis[m - 1][n - 1]) l = mid + 1;
            // include mid
            else r = mid;
        }
        return l;
    }
};

Kotlin

Written by @wingkwong

class Solution {
    private val dirx = intArrayOf(-1, 0, 0, 1)
    private val diry = intArrayOf(0, 1, -1, 0)
    private fun dfs(heights: Array<IntArray>, vis: Array<BooleanArray>, i: Int, j: Int, mid: Int) {
        vis[i][j] = true
        for (d in 0 until 4) {
            val x = i + dirx[d]
            val y = j + diry[d]
            // if it is out of the target mid, then skip
            if (x < 0 || x >= heights.size || y < 0 || y >= heights[0].size || vis[x][y] || 
                Math.abs(heights[i][j] - heights[x][y]) > mid      
            ) continue
            dfs(heights, vis, x, y, mid)
        }
    }
    fun minimumEffortPath(heights: Array<IntArray>): Int {
        val n = heights.size
        val m = heights[0].size
        // init possible range
        var l = 0
        var r = 1e6.toInt()
        // binary search
        while (l < r) {
            val mid = (l + r) / 2
            val vis = Array(n) { BooleanArray(m) }
            // call dfs to check if the dist can be reached or not
            dfs(heights, vis, 0, 0, mid)
            // exclude mid
            if (!vis[n - 1][m - 1]) l = mid + 1
            // include mid
            else r = mid
        }
        return l
    }
}