2013 - Detect Squares (Medium)

Problem Link

https://leetcode.com/problems/detect-squares/

Problem Statement

You are given a stream of points on the X-Y plane. Design an algorithm that:

Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area. An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.

Implement the DetectSquares class:

DetectSquares() Initializes the object with an empty data structure.
void add(int[] point) Adds a new point point = [x, y] to the data structure.
int count(int[] point) Counts the number of ways to form axis-aligned squares with point point = [x, y] as described above.

Example 1:

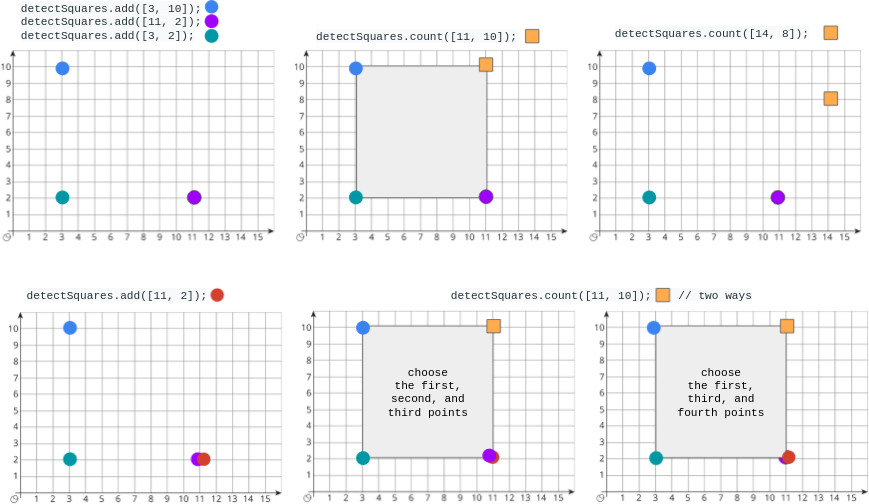
Input
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output
[null, null, null, null, 1, 0, null, 2]

Explanation
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
                               //   - The first, second, and third points
detectSquares.count([14, 8]);  // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]);    // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
                               //   - The first, second, and third points
                               //   - The first, third, and fourth points

Constraints:

point.length == 2
0 <= x, y <= 1000
At most 3000 calls in total will be made to add and count.

Approach 1: Checking for Diagonal Points

This a tricky problem that can be greatly simplified by knowing what to do. If for any given count call, we can check all points inside our hash map and only continue with our algorithm if the point is directly diagonal with the point we are given, then we know we can only create a square with those two points, if there are 2 points that are adjacent to those points, to create the other 2 corners.

Meaning during our search for diagonal points, we want a difference in $x,y$ that is a $dx, dy$ where $dx != dy$ and the $x$ and $y$ values of our potential diagonal points aren't equal, otherwise, that means they are on the same axis.

When we find a suitable corner, we can check the adjacent positions where a corner would need to exist to create a square and multiply the number of points of all three corners to add to our total result. Obviously, if any of those corners don't exist, we will multiply by $0$ , not creating a square.

Time Complexity:

Add: $O(1)$ , we can add points to our data structure in constant time.
Count: $O(n)$ , where $n$ is the number of unique points. We are going to check through all unique points once, doing constant time work to determine if we can create a square, and increment our count for the number of squares we find.

Space Complexity: $O(n)$ where $n$ is the number of unique points. We are going to maintain a hash map for our data structure, only creating keys for unique points, and incrementing a value for those points if we find duplicates.

Python

Written by @ColeB2

class DetectSquares:
    # DetectSquares
    # add O(1) time
    # count O(n) time
    # class will maintain a hashmap of O(n) size.
    def __init__(self):
        # intiialize our hashmap of points
        # key: tuple (x,y) coordinate
        # value: number of times point exists in the plane.
        self.points = {}
        
    def add(self, point: List[int]) -> None:
        # convert our point to a tuple, so it is hashable in python
        point = tuple(point)
        # check point exists in our hash map.
        if point not in self.points:
            # doesn't create the key and initialize value to 0
            self.points[point] = 0
        # increment the value of the given point
        self.points[point] += 1
        
    def count(self, point: List[int]) -> int:
        # initialize square, which is the number of squares
        # we can create with the given point, point.
        squares = 0
        # initialize a px, py to represent the x and y coordinates of
        # the given point, point.
        px, py = point
        # loop through all unique points in our hash map, tracking x, y.
        for (x, y) in self.points.keys():
            # calculate the absolute distance between given point and
            # the unique points in our hash map.
            dx, dy = abs(px - x), abs(py - y)
            # check if points are diagonal apart, if not continue
            # if the dy and dx aren't the same, or if the points exist
            # on the same x/y axis, then they can't be diagonal apart.
            if (dy != dx) or  px == x or py == y:
                continue
            # points are diagonal apart --> check adj corners exist.
            # if a corner exists, we will use the count from our 
            # self.points hash map, otherwise initialize it with 0.
            corner1 = self.points[(x, py)] if (x, py) in self.points else 0
            corner2 = self.points[(px, y)] if (px, y) in self.points else 0
            # add the values of all 3 points that exist in the hash map
            # multiplied together. If one of the corners is a 0, we can't
            # make a square, so it will add 0 to our squares variable.
            squares += corner1 * corner2 * self.points[(x,y)]
        return squares

Problem Link​

Problem Statement​

Approach 1: Checking for Diagonal Points​

Problem Link

Problem Statement

Approach 1: Checking for Diagonal Points