2017 - Grid Game (Medium)

Problem Link

https://leetcode.com/problems/grid-game/

Problem Statement

You are given a 0-indexed 2D array grid of size 2 x n, where grid[r][c] represents the number of points at position (r, c) on the matrix. Two robots are playing a game on this matrix.

Both robots initially start at (0, 0) and want to reach (1, n-1). Each robot may only move to the right ((r, c) to (r, c + 1)) or down ((r, c) to (r + 1, c)).

At the start of the game, the first robot moves from (0, 0) to (1, n-1), collecting all the points from the cells on its path. For all cells (r, c) traversed on the path, grid[r][c] is set to 0. Then, the second robot moves from (0, 0) to (1, n-1), collecting the points on its path. Note that their paths may intersect with one another.

The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot.

Example 1:

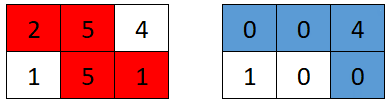
Input: grid = [[2,5,4],[1,5,1]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 0 + 4 + 0 = 4 points.

Example 2:

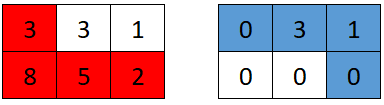
Input: grid = [[3,3,1],[8,5,2]]
Output: 4
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 3 + 1 + 0 = 4 points.

Example 3:

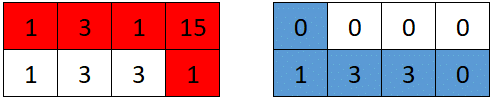
Input: grid = [[1,3,1,15],[1,3,3,1]]
Output: 7
Explanation: The optimal path taken by the first robot is shown in red, and the optimal path taken by the second robot is shown in blue.
The cells visited by the first robot are set to 0.
The second robot will collect 0 + 1 + 3 + 3 + 0 = 7 points.

Constraints:

• grid.length == 2
• n == grid[r].length
• 1 <= n <= 5 * 10^4
• 1 <= grid[r][c] <= 10^5

Approach 1: Prefix & Suffix Sum

The first observation is that the first point on the top row and the last point on the bottom row would be collected by robot 1. Therefore, robot 2 can only collect some from the top or from the bottom. In this case, we can use prefix sum and suffix sum to get how many points robot 2 can collect at a certain index.

For each index $i$, robot 2 could either

• get from the top row, i.e. $pref[n - 1] - pref[i]$, or
• get from the bottom row, i.e. $suff[0] - suff[i]$

We take the maximum one at each $i$ and compare with the current answer. As robot 1 plays optimally, which means it would get the maximum point. We take the minimum here.

Written by @wingkwong

class Solution {
public:
    long long gridGame(vector<vector<int>>& grid) {
        int n = grid[0].size();
        // build pref sum
        vector<long long> pref(n);
        pref[0] = grid[0][0];
        for (int i = 1; i < n; i++) {
            pref[i] = pref[i - 1] + grid[0][i];
        }
        // build suffix sum
        vector<long long> suff(n);
        suff[n - 1] = grid[1][n - 1];
        for (int i = n - 2; i >= 0; i--) {
            suff[i] = suff[i + 1] + grid[1][i];
        }
        // robot 1 would get the max point
        long long ans = 1e18;
        // iterate each index
        for (int i = 0; i < n; i++) {
            // either take 
            ans = min({
                // take the min one with ans
                ans, 
                // choose the best one
                max(
                    // take from the top row
                    pref[n - 1] - pref[i], 
                    // take from the bottom row
                    suff[0] - suff[i])}
                );
        }
        return ans;
    }
};

Further Question 1: What is the maximum points collected by robot 1?

Check Answer

The idea is similar. Robot 1 can collect all points till $i$, then move to the bottom row and go till the end. We can simply check $pref[i]$ (collected on the top row) plus $suff[i]$ (collected on the bottom row).

Written by @wingkwong

class Solution {
public:
    long long gridGame(vector<vector<int>>& grid) {
        int n = grid[0].size();
        vector<int> pref(n);
        pref[0] = grid[0][0];
        for (int i = 1; i < n; i++) {
            pref[i] = pref[i - 1] + grid[0][i];
        }
        vector<int> suff(n);
        suff[n - 1] = grid[1][n - 1];
        for (int i = n - 2; i >= 0; i--) {
            suff[i] = suff[i + 1] + grid[1][i];
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            ans = max(ans, pref[i] + suff[i]);
        }
        return ans;
    }
};

Further Question 2: Are you able to optimise the above solution?