2250 - Count Number of Rectangles Containing Each Point (Medium)

Problem Link

https://leetcode.com/problems/count-number-of-rectangles-containing-each-point/

Problem Statement

You are given a 2D integer array rectangles where rectangles[i] = [li, hi] indicates that ith rectangle has a length of li and a height of hi. You are also given a 2D integer array points where points[j] = [xj, yj] is a point with coordinates (xj, yj).

The ith rectangle has its bottom-left corner point at the coordinates (0, 0) and its top-right corner point at (li, hi).

Return an integer array count of length points.length where count[j] is the number of rectangles that contain the jth point.

The ith rectangle contains the jth point if 0 <= xj <= li and 0 <= yj <= hi. Note that points that lie on the edges of a rectangle are also considered to be contained by that rectangle.

Example 1:

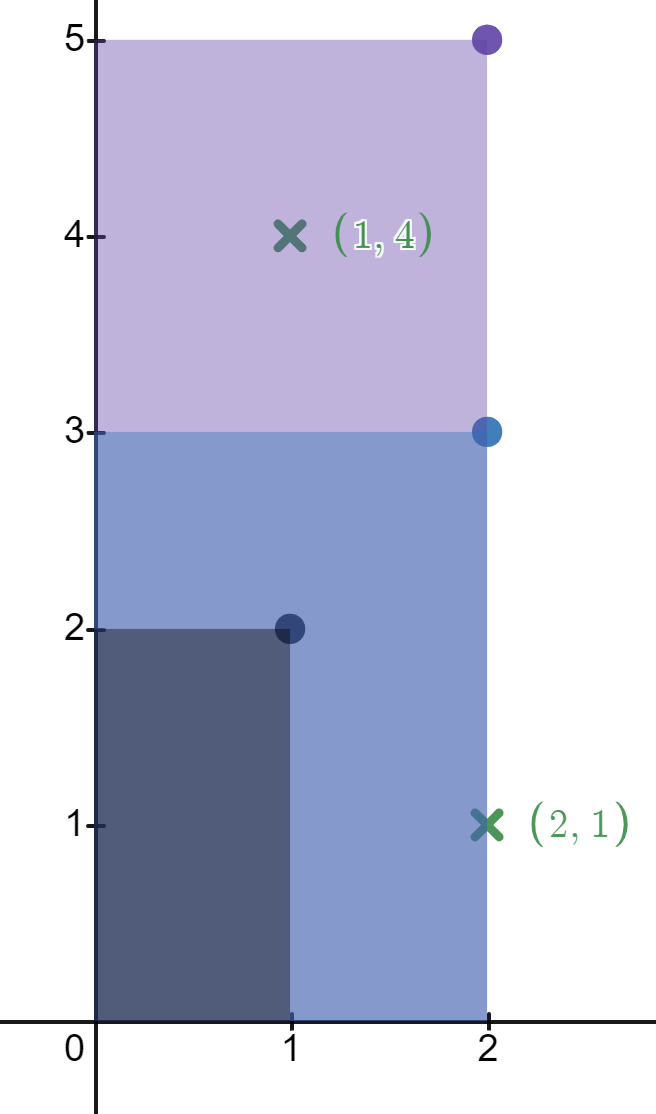
Input: rectangles = [[1,2],[2,3],[2,5]], points = [[2,1],[1,4]]
Output: [2,1]
Explanation:
The first rectangle contains no points.
The second rectangle contains only the point (2, 1).
The third rectangle contains the points (2, 1) and (1, 4).
The number of rectangles that contain the point (2, 1) is 2.
The number of rectangles that contain the point (1, 4) is 1.
Therefore, we return [2, 1].

Example 2:

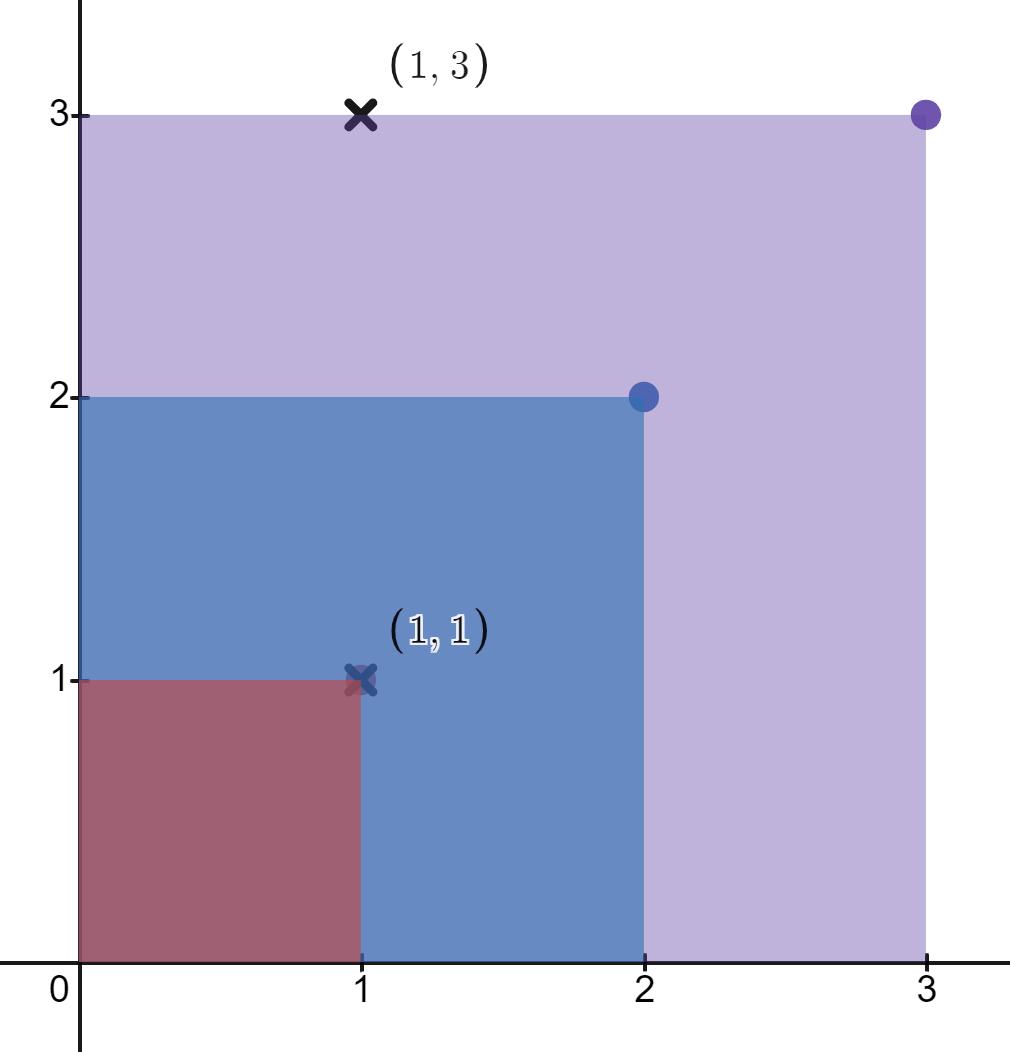
Input: rectangles = [[1,1],[2,2],[3,3]], points = [[1,3],[1,1]]
Output: [1,3]
Explanation:
The first rectangle contains only the point (1, 1).
The second rectangle contains only the point (1, 1).
The third rectangle contains the points (1, 3) and (1, 1).
The number of rectangles that contain the point (1, 3) is 1.
The number of rectangles that contain the point (1, 1) is 3.
Therefore, we return [1, 3].

Constraints:

• 1 <= rectangles.length, points.length <= 5 * 10^4
• rectangles[i].length == points[j].length == 2
• 1 <= li, xj <= 10^9
• 1 <= hi, yj <= 100
• All the rectangles are unique.
• All the points are unique.

Approach 1: Lower Bound

Observation: The max $y$ is only $100$, while the max $x$is $10^9$.

For each $y$, we push the corresponding $x$ and then we sort all the $x$s for each $y$.

Then iterate each point, and iterate from $p_y$ to $max_y$to check how many points are greater than $p_x$.

Written by @wkw

class Solution {
public:
    vector<int> countRectangles(vector<vector<int>>& rectangles, vector<vector<int>>& points) {
        int mxY = 101;
        vector<int> ans;
        vector<vector<int>> m(mxY);
        // use y as a key
        for (auto& r : rectangles) m[r[1]].push_back(r[0]);
        // sort m[i]
        for (int i = 0; i < mxY; i++) sort(m[i].begin(), m[i].end());
        // iterate each point
        for (auto& p : points) {
            int cnt = 0;
            // iterate from p[1] to mxY
            // as these points are covering p[1]
            for (int y = p[1]; y < mxY; y++) {
                // find the first position that p[0] can fit into
                // elements behind this position can form rectangles
                // covering (p[0], p[1])
                cnt += m[y].end() - lower_bound(m[y].begin(), m[y].end(), p[0]);
            }
            // push the result to ans
            ans.push_back(cnt);
        }
        return ans;
    }
};