2218 - Maximum Value of K Coins From Piles (Hard)

Problem Link

https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/

Problem Statement

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

Example 1:

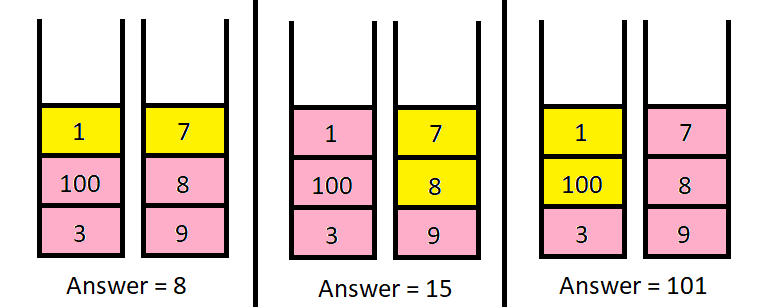
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

Constraints:

• n == piles.length
• 1 <= n <= 1000
• 1 <= piles[i][j] <= 10^5
• 1 <= k <= sum(piles[i].length) <= 2000

Approach 1: Dynamic Programming

Let $dp[i][j]$ be the maximum total value we can have if we pick $j$ elements starting from $piles[i]$. The answer is $dp[0][k]$. First we calculate the value if we pick any elements in the current pile. Then we try to pick at most $min((int) piles[i].size(), k)$ elements and find out the max result.

C++

Written by @wingkwong

class Solution {
public:
    int maxValueOfCoins(vector<vector<int>>& piles, int k) {
        int n = piles.size();
        vector<vector<int>> dp(n, vector<int>(k + 1, -1));
        function<int(int,int)> dfs = [&](int i, int k) {
            // reach the end - return 0
            if (i == n || k == 0) return 0;
            // calculated previously - return immediately
            if (dp[i][k] != -1) return dp[i][k];
            // do not take 
            int res = dfs(i + 1, k), val = 0;
            // try to take it one by one 
            // calculate the value we could have
            for (int j = 0; j < min((int) piles[i].size(), k); j++) {
                // take this element
                val += piles[i][j];
                res = max(res, dfs(i + 1, k - 1 - j) + val);
            }
            return dp[i][k] = res;
        };
        return dfs(0, k);
    }
};

Python

Written by @wingkwong

class Solution:
    def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:
        @lru_cache(None)
        def dp(i, k):
            # reach the end - return 0
            if i == len(piles) or k == 0:
                return 0
            res = 0
            # do not take 
            res += dp(i + 1, k)
            # try to take it one by one 
            # calculate the value we could have
            take = 0
            for j in range(min(k, len(piles[i]))):
                # take this element
                take += piles[i][j]
                res = max(res, dp(i + 1, k - 1 - j) + take)
            return res
        return dp(0, k)