0787 - Cheapest Flights Within K Stops (Medium)

Problem Link

https://leetcode.com/problems/cheapest-flights-within-k-stops/

Problem Statement

There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.

You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return __ -1.

Example 1:

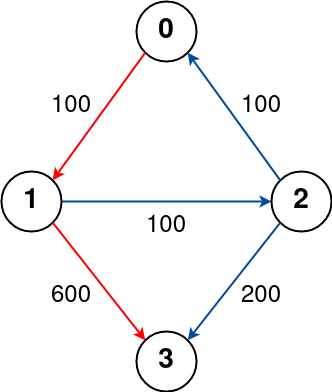
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
Output: 700
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700.
Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.

Example 2:

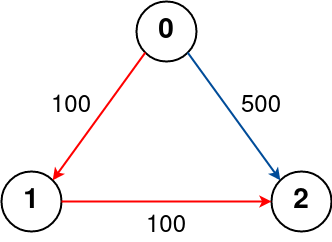
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph is shown above.
The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.

Example 3:

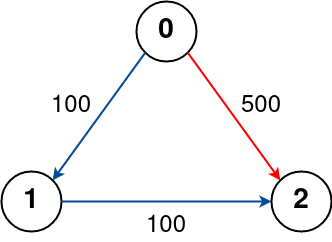
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph is shown above.
The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.

Constraints:

• 1 <= n <= 100
• 0 <= flights.length <= (n * (n - 1) / 2)
• flights[i].length == 3
• 0 <= fromi, toi < n
• fromi != toi
• 1 <= pricei <= 10^4
• There will not be any multiple flights between two cities.
• 0 <= src, dst, k < n
• src != dst

Approach 1: DP

C++

Written by @wingkwong

// TC: O(F * K)
// SC: O(N * K) 
// where 
// - F is the number of flights
// - K is the number of stops
// - N is the number of cities and K is the number of stops
class Solution {
public:
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        // dp[i][j]: min cost to reach city j using at most i edges from src
        vector<vector<int>> dp(k + 2, vector<int>(n, INT_MAX));
        // base case
        for (int i = 0; i <= k + 1; i++) dp[i][src] = 0;
        // iterate each stop
        for (int i = 1; i <= k + 1; i++) {
            // iterate each flight
            for (auto f : flights) {
                int from = f[0], to = f[1], cost = f[2];
                // ensure city `from` is reachable 
                if (dp[i - 1][from] != INT_MAX) {
                    // from + cost -> to
                    dp[i][to] = min(dp[i][to], dp[i - 1][from] + cost);   
                }
            }
        }
        // if dp[k + 1][dst] == INT_MAX, it means it is unreachable
        // else return the cost
        return dp[k + 1][dst] == INT_MAX ? -1 : dp[k + 1][dst];
    }
};

Approach 2: Bellman Ford

C++

Written by @wingkwong

// TC: O(F * K + N * K)
// SC: O(F) 
// where 
// - F is the number of flights
// - K is the number of stops
// - N is the number of cities and K is the number of stops
class Solution {
public:
    // https://leetcodethehardway.com/tutorials/graph-theory/bellman-ford-algorithm
    template<typename T_a3, typename T_vector>
    void bellman_ford(T_a3 &g, T_vector &dist, int src, int mx_edges) {
        dist[src] = 0;
        for (int i = 0; i <= mx_edges; i++) {
            T_vector ndist = dist;
            for (auto x : g) {
                auto [from, to, cost] = x;
                ndist[to] = min(ndist[to], dist[from] + cost);
            }
            dist = ndist;
        }
    }
    
    int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) {
        // we can directly use bellman ford template here (prerequisite: you need to understand bellman ford algo)
        // bellman ford algo is used to find the shortest paths from source node to other nodes in a weighted graph
        vector<array<int, 3>> g;
        // initially cost with a large value
        // cost[i] means the cheapest price from src to city i
        vector<int> cost(n, 1e9);
        // reconstruct a bit - {src, dst, cost}
        for (auto f : flights) g.push_back({f[0], f[1], f[2]});
        bellman_ford(g, cost, src, k);
        // if cost[dst] == 1e9, it means it is unreachable
        // else we can show cost[dst]
        return cost[dst] == 1e9 ? -1 : cost[dst];
    }
};

Python

Written by @wingkwong

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        def bellman_ford(g, dist, src, mx_edges):
            dist[src] = 0
            for i in range(mx_edges + 1):
                ndist = dist.copy()
                for x in g:
                    _from, to, cost = x
                    ndist[to] = min(ndist[to], dist[_from] + cost)
                dist = ndist
            return dist
        g = []
        for f in flights:
            g.append([f[0], f[1], f[2]])
        cost = bellman_ford(g, [1e9] * n, src, k)
        if cost[dst] == 1e9:
            return -1
        return cost[dst]

Approach 3: Dijkstra's Algorithm

We can use Dijkstra's Algorithm to find the shortest path. Dijkstra's Algorithm uses a heap for weights of distance we travelled, meaning with a min heap we can always check the path that is currently the shortest. One key difference though is instead of a visited set, we will use a hash map, as we might visit a city early, but run out of stops and a set would prevent us from reaching this city again. So to prevent this we can use a hash map that maps cities to stops, and if we reach a city with fewer stops than last time, we can visit this city again.

Time Complexity: $O((F + C)logC)$ Where $F$ is the number of flights, and $C$ is the number of cities. Worst case we must take all flights and visit all cities, updating our heap $logC$ times at each city.

Space Complexity: $O(C)$ Where $C$ is the number of cities. We must create an adjacency list, a heap, and a visited dictionary, all of which scale proportionally to the number of cities.

Python

Written by @ColeB2

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        # create an adjacency list
        adj_list = [[] for _ in range(n)]
        # adjacenty list will be a list for cities and prices
        # we can fly to from a desitination, i, in the list.
        for from_i, to_i, price_i in flights:
            adj_list[from_i].append((to_i, price_i))
        # heap (price, stops, destination)
        heap = [(0, 0, src)]
        visited = defaultdict(int)

        while heap:
            # pop off the lowest price destination in our heap.
            # Tracking price, # of stops we took, and destination.
            price, stops, dest = heapq.heappop(heap)
            # if we reached the destination, return the total price.
            if dest == dst:
                return price
            # Track the destination as visited, and stops to reach it.
            visited[dest] = stops
            # Loop through all potential flights from current destination.
            for to_i, price_i in adj_list[dest]:
                # stops > k, it means this path doesn't work.
                # also if to destination isn't visited, or it is
                # visited, but the # of stops < # of stops it took us
                # to reach the city the last time:
                if stops <= k and (to_i not in visited or stops < visited[to_i]):
                    # add that destination to the queue.
                    # price, stops, to destination. Where price is the
                    # current running price + price to fly there.
                    # The stops should be incremented by 1, and
                    # the destination is the to_i value.
                    heapq.heappush(heap, (price + price_i, stops + 1, to_i))
        # process everything but never reach destination, return -1
        return -1