0778 - Swim in Rising Water (Hard)

Problem Link

https://leetcode.com/problems/swim-in-rising-water/

Problem Statement

You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).

The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.

Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).

Example 1:

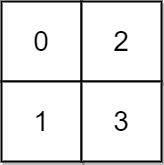
Input: grid = [[0,2],[1,3]]
Output: 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.

Example 2:

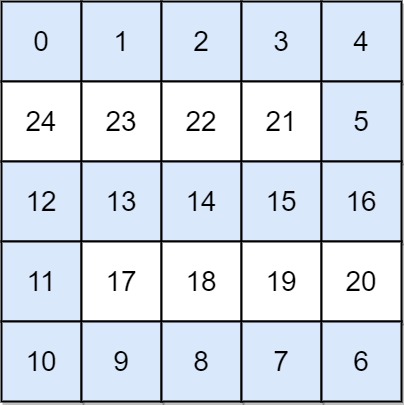
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation: The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] < n2
• Each value grid[i][j] is unique.

Approach 1: Dijkstra's Algorithm

You could imagine that using a breadth-first search, on each iteration we would want to sort the queue by elevation of cells, so as to follow the best path first, instead of all paths. That is where Dijkstra's algorithm comes in.

Dijkstra's algorithm gives us access to the best possible cell to follow inside our path by utilizing a min-heap. The min heap sorts the cells so the lowest elevation cell will always be on top, and by utilizing Dijkstra's algorithm, we guaranteed the best path. We must also maintain a visited set to prevent revisiting any cells.

Time Complexity: $O(n^2 logn)$ Where n is both the height and width of our square grid. At most our heap will contain $n^2$ elements, and to push values on the heap takes $O(logn)$ time.

Space Complexity: $O(n^2)$ as the heap and the visited set may contain up to $n^2$ cells inside of them.

Python

Written by @ColeB2

class Solution:
    def swimInWater(self, grid: List[List[int]]) -> int:
        n = len(grid)
        # heap for dijkstra's algorithm: (height, y, x) where the heap
        # will sort by the first value first, the height and the y,x are
        # the row and column coordinates inside our matrix.
        # note height and time are the same thing, as we must wait t
        # time to travel to a given height.
        heap = [(grid[0][0], 0,0)]
        visited = set()
        directions = ((1,0), (0,1), (-1,0), (0,-1))
        # while we have values inside our heap to follow.
        while heap:
            # pop off our time, and y, x coordinates
            t, y, x = heapq.heappop(heap)
            # if we reach bottom right, return given time.
            if (y,x) == (n-1, n-1):
                return t
            # traverse 4 directionally
            for dy, dx in directions:
                new_y, new_x = y + dy, x + dx
                # boundary and visited cell check.
                if (new_x < 0 or new_x == n
                    or new_y < 0 or new_y == n
                    or (new_y, new_x) in visited
                    ):
                    continue
                # In bound and haven't visited the cell before:
                # add to visited to prevent revisiting said cell.
                visited.add((new_y,new_x))
                # calculate the new time, which will be the largest value
                # of the cell we are looking at, and the time we passed
                # to the last cell.
                # Note, each cell will track the max possible time to 
                # reach said cell. Example: if our (0,0) cell started at
                # t = 20, and the adjacent cells are all < 20, it would
                # no longer matter which cell you travelled to first as
                # you would have to wait for t = 20 anyways.
                new_time = max(grid[new_y][new_x], t)
                # push cell to our heap. (time, y, x)
                heapq.heappush(heap, (new_time, new_y, new_x))