0847 - Shortest Path Visiting All Nodes (Hard)

Problem Link

https://leetcode.com/problems/shortest-path-visiting-all-nodes/

Problem Statement

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

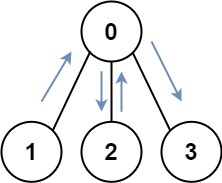
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

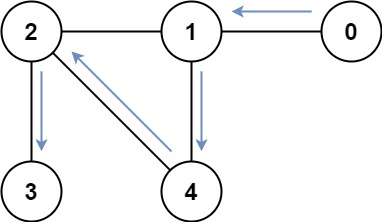
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Constraints:

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] does not contain i.
• If graph[a] contains b, then graph[b] contains a.
• The input graph is always connected.

Approach 1: BFS

There are two key observations in this question

• We can use a bitmask to represent visited nodes as there are at most 12 nodes
• We should use BFS as we want to find the shortest path that visits all nodes

We then need to figure out how to keep track of duplication. We can simply store the (currentNode, visitedBitMask) tuple in a set to prevent duplication.

We can start at any node in the graph initially, and we should update the bitmask accordingly.

Python

Written by @heiheihang

def shortestPathLength(self, graph: List[List[int]]) -> int:
    # a visited set to prevent duplication
    visited = set()
    # number of nodes in the graph
    n = len(graph)
    # we want to visit all nodes (1111...1111)
    target = (1 << n) - 1
    # a level set to keep the states at the current depth
    level = set()
    # we can start at any node initially
    for i in range(n):
        level.add((i, 1 << i))
    # keep track of the distance of the path
    depth = 0
    while (level):
        # store the states in the next level
        new_level = set()
        for node, mask in level:
            # continue if state is visited before
            if (node,mask) in visited:
                continue
            # return depth if all nodes have been visited
            if(mask == target):
                return depth
            # add the current state to visited
            visited.add((node,mask))
            # add the visiting neighbour state to the next level
            for neighbour in graph[node]:
                new_level.add((neighbour, mask | (1 << neighbour)))
        # go to the next level
        level = new_level
        # increase distance by 1
        depth += 1
    # should never reach here
    return -1

Kotlin

Written by @wingkwong

class Solution {
    fun shortestPathLength(graph: Array<IntArray>): Int {
        val n = graph.size
        if (n == 1) {
            return 0
        }
        val q: Queue<IntArray> = LinkedList()
        val vis = Array(n) { BooleanArray((1 shl n) - 1) }
        for (i in 0 until n) {
            q.add(intArrayOf(i, 1 shl i))
            vis[i][1 shl i] = true
        }
        var steps = 0
        while (q.isNotEmpty()) {
            val next_q: Queue<IntArray> = LinkedList()
            for (i in 0 until q.size) {
                val (u, mask) = q.poll()
                for (v in graph[u]) {
                    val next_mask = mask or (1 shl v)
                    if (next_mask == (1 shl n) - 1) {
                        return steps + 1
                    }
                    if (!vis[v][next_mask]) {
                        vis[v][next_mask] = true
                        next_q.add(intArrayOf(v, next_mask))
                    }
                }
            }
            steps++
            q.addAll(next_q)
        }
        return 0
    }
}

Approach 2: Floyd-Warshall & TSP

Since $n$ is small, we can use Floyd–Warshall algorithm to calculate the shortest distances between all pairs of nodes in $O(n ^ 3)$. Let $d[i][j]$ be the distance between node $i$ and node $j$. First we initialise each distance to be infinity or a large number. Then for each edge, we can set the weight (i.e. distance in this case) to $0$ if $i$ is same as $j$, else we can build $d$ based on the input.

Then, we use the below recursive formula to calculate the shortest distances. For details, please check out Floyd-Warshall Algorithm.$shortestPath(i, j, k) = min(shortestPath(i, j, k - 1), shortestPath(i, k, k - 1) + shortestPath(k, j, k - 1))$

What's left is similar to TSP, which is Traveling Salesman Problem. Given a set of nodes and weight between every pair, what is the shortest possible path that visits all nodes exactly once and returns to the starting point? The only difference is that a node is allowed to be visited multiple times and the starting point and the ending point may not be same.

Let $dp[i][mask]$ be the shortest distances with visited nodes (marked as $1$ in $mask$) from the starting point $i$. In our function, first we check if $dp[src][mask]$ has been calculated before. If so, we can return it immediately. Otherwise, let's set this node in $mask$ and compare it with the target mask, which is $(1 << n) - 1$, i.e. all 1s with $n$ digits. If it matches with target mask, that means we visited all the nodes. Hence, we return $0$. Otherwise, we look for the next possible node to visit and calculate the distances recursively. At the end, we memoize the shortest distance at the current state and return it.

Go

Written by @wingkwong

func min(x, y int) int {
    if x < y {
        return x
    }
    return y
}

// Traveling Salesman Problem (TSP)
func tsp(mask int, src int, n int, d [][]int, dp [][]int) int {
    // if dp[src][mask] has been calculated before
    // then just return it
    if dp[src][mask] != -1 {
        return dp[src][mask]
    }
    // mark src visited
    now := mask | (1 << src)
    // the dest is all 1s - meaning all nodes have been visited
    dest := (1 << n) - 1
    // if we viste all nodes, then return 0
    if now == dest {
        return 0
    }
    // init mi as a large number
    mi := 10000000
    for i := 0; i < n; i++ {
        // check for the next possible node to move
        if ((mask & (1 << i)) == 0) {
            // the distance from node src to node i 
            // plus the shortest distance starting from node i
            mi = min(mi, d[src][i] + tsp(now, i, n, d, dp))
        }
    }
    // memoize the shortest distance
    dp[src][mask] = mi
    return dp[src][mask]
}

func shortestPathLength(graph [][]int) int {
    n := len(graph)
    // use floyd-warshall algo to calcuate the shortest distances 
    // between all pairs of nodes
    // d[i][j]: shortest distance between node i and node j
    d := make([][]int, 1 << n)
    // preparing initial d
    for i := 0; i < n; i++ {
        d[i] = make([]int, n)
        for j := 0; j < n; j++ {
            // set the initial weight (distance) to a large number / inf
            d[i][j] = 10000000
        }
    }
    for i := 0; i < n; i++ {
        // if source is same as dest, then the shortest distance is 0
        d[i][i] = 0
        for _, j := range graph[i] {
            // iterate the input to build the distances for each pair
            d[i][j] = 1
        }
    }
    // recusively calculate the shortest distances
    for k := 0; k < n; k++ {
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                d[i][j] = min(d[i][j], d[i][k] + d[k][j])
            }
        }
    }
    // preparing dp for TSP
    dp := make([][]int, n)
    for i := 0; i < n; i++ {
        dp[i] = make([]int, 1 << n)
        for j := 0; j < (1 << n); j++ {
            dp[i][j] = -1
        }
    }
    ans := 10000000
    for i := 0; i < n; i++ {
        // try each i as starting node
        // to find out the min distance
        ans = min(ans, tsp(1 << i, i, n, d, dp))
    }
    return ans
 }