0867 - Transpose Matrix (Easy)
Problem Link
https://leetcode.com/problems/transpose-matrix/
Problem Statement
Given a 2D integer array matrix, return the transpose of matrix.
The transpose of a matrix is the matrix flipped over its main diagonal, switching the matrix's row and column indices.
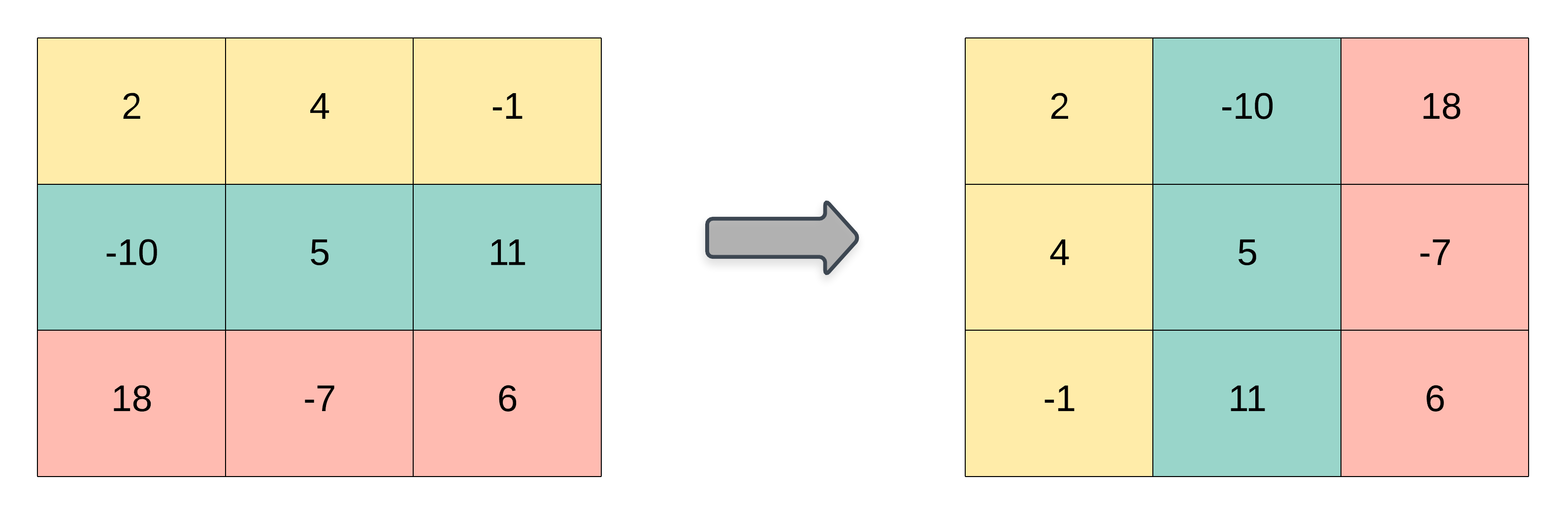
Example 1:
**Input:** matrix = [[1,2,3],[4,5,6],[7,8,9]]
**Output:** [[1,4,7],[2,5,8],[3,6,9]]
Example 2:
**Input:** matrix = [[1,2,3],[4,5,6]]
**Output:** [[1,4],[2,5],[3,6]]
Constraints:
Approach 1: Iterating over the columns and rows
The solution used was iterating over the columns and rows of the original matrix switching their indexes and creating a new row for each column from the original matrix in order to obtain its transposed matrix.
For example, consider the given matrix as the input. Starting from the first element of the first column we assign it to the first element of the first row of the transposed matrix . Then we go to the second element of the first column and assign it to the second element of the first row of the transposed matrix . And we repeat this process for every column of the original matrix until we get the final result of which will be .
- Python
- JavaScript
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
transposed = []
for row in range(len(matrix[0])):
transposed.append([])
for column in range(len(matrix)):
transposed[row].append(matrix[column][row])
return transposed
class Solution:
def transpose(self, matrix: List[List[int]]) -> List[List[int]]:
return [[matrix[row][col] for row in range(0, len(matrix))] for col in range(0, len(matrix[0]))]
const transpose = (matrix) => {
const transposed = [];
for (const row in matrix[0]) {
transposed.push([]);
for (const column of matrix) {
transposed[row].push(column[row]);
}
}
return transposed;
};
Time Complexity:
The time complexity for this solution is considering as the number of rows and as the number of columns in the original matrix.
Space Complexity:
The space complexity for this solution is also considering as the number of rows and as the number of columns in the original matrix.