1443 - Minimum Time to Collect All Apples in a Tree (Medium)

Problem Link

https://leetcode.com/problems/minimum-time-to-collect-all-apples-in-a-tree/

Problem Statement

Given an undirected tree consisting of n vertices numbered from 0 to n-1, which has some apples in their vertices. You spend 1 second to walk over one edge of the tree. Return the minimum time in seconds you have to spend to collect all apples in the tree, starting at vertex 0 and coming back to this vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi. Additionally, there is a boolean array hasApple, where hasApple[i] = true means that vertex i has an apple; otherwise, it does not have any apple.

Example 1:

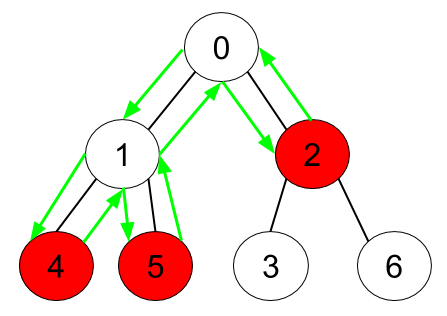
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,true,true,false]
Output: 8
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 2:

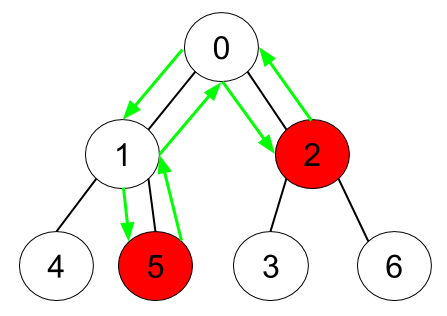
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,true,false,false,true,false]
Output: 6
Explanation: The figure above represents the given tree where red vertices have an apple. One optimal path to collect all apples is shown by the green arrows.

Example 3:

Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], hasApple = [false,false,false,false,false,false,false]
Output: 0

Constraints:

• 1 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai < bi <= n - 1
• fromi < toi
• hasApple.length == n

Approach 1: DFS + Backtracking

1. Let's make another array out of edges and call it graph, where each element graph[i] contains neighbour edges.
2. Perform DFS + backtracking to calculate the minimum time in second using graph.

Time Complexity: $O(n)$

Space Complexity: $O(n)$

Python

Written by @hirotake111

class Solution:
    def minTime(self, n: int, edges: List[List[int]], hasApple: List[bool]) -> int:
        # Edge case: no apples - just return 0
        if len(list(filter(lambda edge: edge, hasApple))) == 0:
            return 0

        # Create a graph using edges
        graph: List[List[int]] = [[] for _ in range(n)]
        for edge_a, edge_b in edges:
            if edge_b not in graph[edge_a]:
                graph[edge_a].append(edge_b)
            if edge_a not in graph[edge_b]:
                graph[edge_b].append(edge_a)

        def dfs(current: int, parent: int) -> int:
            sub_total = 0

            for child in graph[current]:
                # If child == parent, do nothing to prevent going back to the parent
                # If not, this should be an index of a child edge
                # -> perform dfs and add the result to sub total
                if child != parent:
                    sub_total += dfs(child, current)

            # If the edge has apples in it, or  if children has apples,
            # we need to visit it -> add extra 2
            if hasApple[current] or 0 < sub_total:
                return sub_total + 2
            # Else, this edge has no apples, or no children that have apples.
            # So we don't have to visit this edge -> just return 0
            return 0

        # In this approach dfs() assumes there is always a parent edge connected to it.
        # But since root doesn't have it - the result has 2 extra unit of seconds.
        # Therefore subtract 2 from the result of dfs()
        return dfs(0, -1) - 2

Go

Written by @hirotake111

func minTime(n int, edges [][]int, hasApple []bool) int {
	// Edge case: no nodes containing apple
	flag := false
	for _, apple := range hasApple {
		flag = flag || apple
	}
	if !flag {
		return 0
	}

	// Create a graph
	graph := make([][]int, n)
	for _, edgeIndexes := range edges {
		edgeA := edgeIndexes[0]
		edgeB := edgeIndexes[1]
		if !contains(graph[edgeA], edgeB) {
			graph[edgeA] = append(graph[edgeA], edgeB)
		}
		if !contains(graph[edgeB], edgeA) {
			graph[edgeB] = append(graph[edgeB], edgeA)
		}
	}

	var dfs func(current, parent int) int
	dfs = func(current, parent int) int {
		subTotal := 0
		for _, child := range graph[current] {
			if child != parent {
				// child index points to a child edge
				subTotal += dfs(child, current)
			}
		}
		if hasApple[current] || 0 < subTotal {
			return subTotal + 2
		}
		return 0
	}

	return dfs(0, -1) - 2
}

func contains(edges []int, target int) bool {
	for edge := range edges {
		if edge == target {
			return true
		}
	}
	return false
}

C++

Written by @wingkwong

class Solution {
public:
    int minTime(int n, vector<vector<int>>& edges, vector<bool>& hasApple) {
        vector<vector<int>> g(n);
        for (auto x : edges) {
            g[x[0]].push_back(x[1]);
            g[x[1]].push_back(x[0]);
        }
        // u = currenct vertex
        // p = parent vertex
        function<int(int, int)> dfs = [&] (int u, int p) {
            int res = 0, t = 0;
            for (auto v : g[u]) {
                // if v is not same as p
                if (p ^ v) {
                    // calculate the child time
                    t = dfs(v, u);
                    // if there is an apple in the subtree, we need 2 seconds to collect it and head back
                    // if we are in vertex 1, we need 4 seconds to collect all the apples in 4 & 5 
                    // i.e. (1 -> 4, 4 -> 1, 1 -> 5, 5 -> 1)
                    // how does 0 know that 1 has collected the apple? check the time, i.e. `t`
                    // if t > 0, it means we got some apples in sub trees
                    if (t > 0 || hasApple[v]) {
                        res += t + 2;
                    }
                }
            }
            return res;
        };
        return dfs(0, -1);
    }
};