1494 - Parallel Courses II (Hard)

Problem Link

https://leetcode.com/problems/parallel-courses-ii

Problem Statement

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei. Also, you are given the integer k.

In one semester, you can take at most k courses as long as you have taken all the prerequisites in the previous semesters for the courses you are taking.

Return the minimum number of semesters needed to take all courses. The testcases will be generated such that it is possible to take every course.

Example 1:

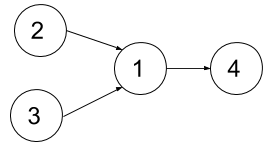
Input: n = 4, dependencies = [[2,1],[3,1],[1,4]], k = 2
Output:
 3
Explanation:
 The figure above represents the given graph.
In the first semester, you can take courses 2 and 3.
In the second semester, you can take course 1.
In the third semester, you can take course 4.

Example 2:

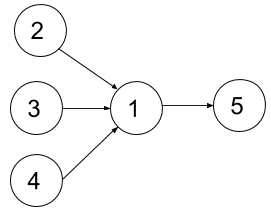
Input: n = 5, dependencies = [[2,1],[3,1],[4,1],[1,5]], k = 2
Output:
 4
Explanation:
 The figure above represents the given graph.
In the first semester, you can take courses 2 and 3 only since you cannot take more than two per semester.
In the second semester, you can take course 4.
In the third semester, you can take course 1.
In the fourth semester, you can take course 5.

Example 3:

Input: n = 11, dependencies = [], k = 2
Output:
 6

Constraints:

• 1 <= n <= 15
• 1 <= k <= n
• 0 <= relations.length <= n * (n-1) / 2
• relations[i].length == 2
• 1 <= prevCoursei, nextCoursei <= n
• prevCoursei != nextCoursei
• All the pairs [prevCoursei, nextCoursei] are unique.
• The given graph is a directed acyclic graph.

Approach 1: DP Bit Masking

Written by @wingkwong

class Solution {
public:
    int minNumberOfSemesters(int n, vector<vector<int>>& dependencies, int k) {
        // dp[i] : the minimum number of semesters needed to take the courses with the bit set in i
        // the worst case is that in each semester we can only take one course, hence initialise with `n`
        // at the end, the answer would be dp[(1 << n) - 1], i.e. all bits set
        vector<int> dp(1 << n, n);
        // if the i-th bit is set in pre[j], 
        // that means we need to take course i in order to take course j
        vector<int> pre(n);
        // build the prerequisites
        for (auto& x : dependencies) {
            // make it 0-based index
            --x[0], --x[1];
            // set the bit at x[0]-th place
            pre[x[1]] |= 1 << x[0];
        }
        // base case: 0 semester. 0 course.
        dp[0] = 0;
        // i is a set of courses that we've already studied
        for (int i = 0; i < (1 << n); i++) {
            // init can as 0 to record how can courses we can study
            int can = 0;
            // iterate all courses
            for (int j = 0; j < n; j++) {
                // check if we've studied prerequisite courses
                if ((pre[j] & i) == pre[j]) {
                    // if so, we can study course j
                    can |= (1 << j);
                }
            }
            // remove those courses that we've already studied
            can &= ~i;
            // enumerate all the bit 1 combinations of `can`
            // i.e. all subsets of a bit representation
            for (int s = can; s ; s = (s - 1) & can) {
                // check if we can take __builtin_popcount(s) courses
                if (__builtin_popcount(s) <= k) {
                    // if so, we combine the previous results (what've studied already)
                    // or we take a new semester
                    dp[i | s] = min(dp[i | s], dp[i] + 1);
                }
            }
        }
        // same as dp[(1 << n) - 1]
        return dp.back();
    }
};