Skip to main content

2331 - Evaluate Boolean Binary Tree (Easy)

https://leetcode.com/problems/evaluate-boolean-binary-tree

Problem Statement​

You are given the root of a full binary tree with the following properties:

  • Leaf nodes have either the value 0 or 1, where 0 represents False and 1 represents True.
  • Non-leaf nodes have either the value 2 or 3, where 2 represents the boolean OR and 3 represents the boolean AND.

The evaluation of a node is as follows:

  • If the node is a leaf node, the evaluation is the value of the node, i.e. True or False.
  • Otherwise, evaluate the node's two children and apply the boolean operation of its value with the children's evaluations.

Return the boolean result of evaluating the root node.

A full binary tree is a binary tree where each node has either 0 or 2 children.

A leaf node is a node that has zero children.

Example 1:

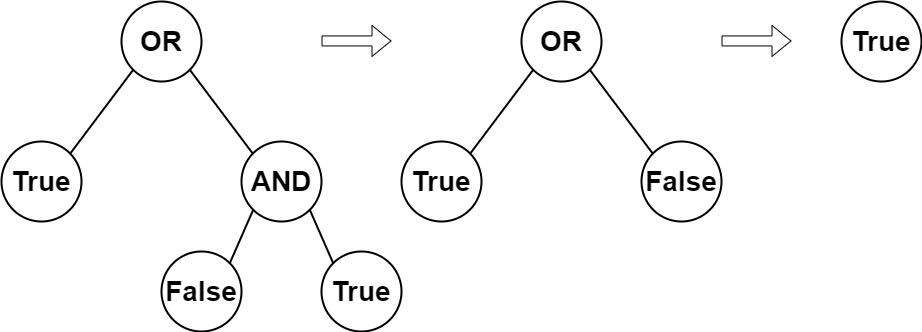
Input: root = [2,1,3,null,null,0,1]
Output: true
Explanation: The above diagram illustrates the evaluation process.
The AND node evaluates to False AND True = False.
The OR node evaluates to True OR False = True.
The root node evaluates to True, so we return true.

Example 2:

Input: root = [0]
Output: false
Explanation: The root node is a leaf node and it evaluates to false, so we return false.

Constraints:

  • The number of nodes in the tree is in the range [1, 1000].
  • 0 <= Node.val <= 3
  • Every node has either 0 or 2 children.
  • Leaf nodes have a value of 0 or 1.
  • Non-leaf nodes have a value of 2 or 3.

Approach 1: Recursive​

We have four cases:

  1. If the value is 0, then return false
  2. If the value is 1, then return true
  3. If the value is 2, then call the function on left tree and right tree and apply OR operation on both returned values
  4. If the value is 3, then call the function on left tree and right tree and apply AND operation on both returned values
Written by @wingkwong
class Solution {
public:
    bool evaluateTree(TreeNode* root) {
        // case 1
        if (root->val == 0) return false;
        // case 2
        else if (root->val == 1) return true;
        // case 3
        else if (root->val == 2) return evaluateTree(root->left) || evaluateTree(root->right);
        // case 4
        return evaluateTree(root->left) && evaluateTree(root->right);
    }
};