Skip to main content

2360 - Longest Cycle in a Graph (Hard)

https://leetcode.com/problems/longest-cycle-in-a-graph

Problem Statement​

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.

Return the length of the longest cycle in the graph. If no cycle exists, return -1.

A cycle is a path that starts and ends at the same node.

Example 1:

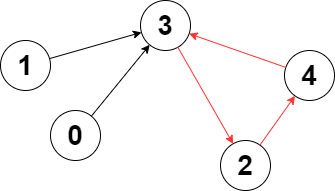
Input: edges = [3,3,4,2,3]
Output: 3
Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2.
The length of this cycle is 3, so 3 is returned.

Example 2:

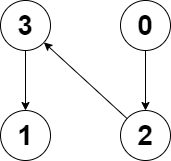
Input: edges = [2,-1,3,1]
Output: -1
Explanation: There are no cycles in this graph.

Constraints:

  • n == edges.length
  • 2 <= n <= 10^5
  • -1 <= edges[i] < n
  • edges[i] != i

Approach: Strongly Connected Component​

We can compute Strongly Connected Component on the graph and find the maximum one.

Written by @wingkwong
class Solution {
public:
    struct SCC : vector<int> {
      vector<vector<int>> comps;
      vector<int> S;

      SCC() {}
      SCC(vector<vector<int>>& G) : vector<int>((int)G.size(), -1), S((int)G.size()) {
        for(int i = 0; i < (int)G.size(); i++) if(!S[i]) dfs(G, i);
      }

      int dfs(vector<vector<int>>& G, int v) {
        int low = S[v] = (int)S.size();
        S.push_back(v);
        for(auto e : G[v]) if(at(e) < 0) low = min(low, S[e] ?: dfs(G, e));
        if(low == S[v]) {
          comps.push_back({});
          for(int i = S[v]; i < (int)S.size(); i++) {
            at(S[i]) = (int)comps.size() - 1;
            comps.back().push_back(S[i]);
          }
          S.resize(S[v]);
        }
        return low;
      }
    };
    
    int longestCycle(vector<int>& edges) {
        int n = edges.size(), ans = -1;
        vector<vector<int>> g(n);
		// we only need those nodes with outgoing edge
        for (int i = 0; i < n; i++) if (edges[i] != -1) g[i].push_back(edges[i]);
		// compute strongly connected components
        SCC s = SCC(g);
		// if the size is greater than 1, that means there is a cycle (which has at least two nodes)
		// so iterate each possible answer and find the max one
        for (auto &x : s.comps) if ((int) x.size() > 1) ans = max(ans, (int) x.size());
        return ans;
    }
};