Skip to main content

2359 - Find Closest Node to Given Two Nodes (Medium)

https://leetcode.com/problems/find-closest-node-to-given-two-nodes

Problem Statement​

You are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.

The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from i, then edges[i] == -1.

You are also given two integers node1 and node2.

Return the index of the node that can be reached from both node1 and node2, such that the maximum between the distance from node1 to that node, and from node2 to that node is minimized. If there are multiple answers, return the node with the smallest index, and if no possible answer exists, return -1.

Note that edges may contain cycles.

Example 1:

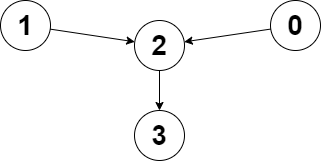
Input: edges = [2,2,3,-1], node1 = 0, node2 = 1
Output: 2
Explanation: The distance from node 0 to node 2 is 1, and the distance from node 1 to node 2 is 1.
The maximum of those two distances is 1. It can be proven that we cannot get a node with a smaller maximum distance than 1, so we return node 2.

Example 2:

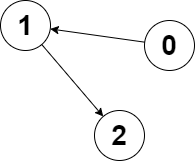
Input: edges = [1,2,-1], node1 = 0, node2 = 2
Output: 2
Explanation: The distance from node 0 to node 2 is 2, and the distance from node 2 to itself is 0.
The maximum of those two distances is 2. It can be proven that we cannot get a node with a smaller maximum distance than 2, so we return node 2.

Constraints:

  • n == edges.length
  • 2 <= n <= 10^5
  • -1 <= edges[i] < n
  • edges[i] != i
  • 0 <= node1, node2 < n

Approach 1: DFS x 2​

Since there is only at most 1 outgoing edge, we can simply use DFS.

Written by @wingkwong
class Solution {
public:
    void dfs(int u, vector<int>& d, vector<int>& vis, vector<int>& edges) {
        // mark it visited
        vis[u] = 1;
        // check the outgoing edge
        int v = edges[u];
        // -1 means there is no outgoing edge, so we skip it
        // if it is visited, we also skip it
        if (v != -1 && !vis[v]) {
            // the dist going to node v form node u is simply d[u] + 1
            d[v] = d[u] + 1;
            // dfs on neigbour node `v`
            dfs(v, d, vis, edges);
        }
    }
    
    int closestMeetingNode(vector<int>& edges, int node1, int node2) {
        int n = edges.size();
        // d1[i]: shortest dist to node i starting from node 1
        // d2[i]: shortest dist to nodes i starting from node 2
        vector<int> d1(n, INT_MAX), d2(n, INT_MAX);
        // vis1[i]: true if node i is visited else false. used for building d1
        // vis2[i]: true if node i is visited else false. used for building d2
        vector<int> vis1(n, 0), vis2(n, 0);
        // dist to node1 from node1 is 0, same as node2 
        d1[node1] = 0, d2[node2] = 0;
        // build the dist for d1
        dfs(node1, d1, vis1, edges);
        // build the dist for d2
        dfs(node2, d2, vis2, edges);
        // iterate each node to find the min max dist
        int ans = -1, mi = INT_MAX;
        for (int i = 0; i < n; i++) {
            if (max(d1[i], d2[i]) < mi) {
                mi = max(d1[i], d2[i]);
                ans = i;
            }
        }
        return ans;
    }
};

Approach: Dijkstra x 2​

Dijkstra approach in this question is not recommended but here's how we do in case there are multiple outgoing edges.

Written by @wingkwong
class Solution {
public:
    // https://leetcodethehardway.com/tutorials/graph-theory/dijkstra
    template<typename T_pair, typename T_vector>
    void dijkstra(T_pair &g, T_vector &dist, int start) {
      priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
      dist[start] = 0;
      pq.push({start, 0});
      while (!pq.empty()) {
        auto [u_node, u_cost] = pq.top(); pq.pop();
        if (u_cost > dist[u_node]) continue;
        for (auto [v_node, v_cost] : g[u_node]) {
          if (dist[v_node] > dist[u_node] + v_cost) {
            dist[v_node] = dist[u_node] + v_cost;
            pq.push({v_node, dist[v_node]});
          }
        }
      }
    }
    
    int closestMeetingNode(vector<int>& edges, int node1, int node2) {
        int n = edges.size();
        // d1[i]: shortest dist to node i starting from node 1
        // d2[i]: shortest dist to nodes i starting from node 2
        vector<int> d1(n, INT_MAX), d2(n, INT_MAX);
        // build the graph
        vector<vector<pair<int, int>>> g(n);
        // iterate each node
        for (int i = 0; i < n; i++) {
            // if there is outgoing edge from node i
            if (edges[i] != -1) {
                // by default, we define the dist to edges[i] is 1
                g[i].push_back({edges[i], 1});
            }
        }
        // build the dist for d1
        dijkstra(g, d1, node1);
        // build the dist for d2
        dijkstra(g, d2, node2);
        // iterate each node to find the min max dist
        int ans = -1, mi = INT_MAX;
        for (int i = 0; i < n; i++) {
            if (max(d1[i], d2[i]) < mi) {
                mi = max(d1[i], d2[i]);
                ans = i;
            }
        }
        return ans;
    }
};