Introduction

OverviewCopy Anchor Link

A graph is made up of a collection of points or objects called vertices and connections between some of those vertices called edges. The edges can be either one-way (can only be traversed in one direction), two-way, have a numerical value associated with traversing them, or without any value. We can use graphs to solve a plethora of interesting problems!

Here is a undirected graph with 4 vertices (or nodes) and 5 edges.

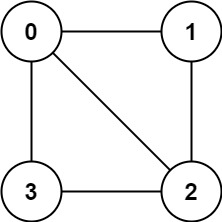
ExampleCopy Anchor Link

In real life, we may use graphs. Let's say we have six people:

• Alice
• Bob
• Cathy
• Danny
• Ethan
• Fiona

and we are also given a list of friends.

[["Alice", Bob"], ["Cathy", "Danny"], ["Alice", "Cathy"], ["Ethan", "Fiona"]]

Here, we know that:

• Alice and Bob are friends
• Cathy and Danny are friends
• Alice and Cathy are friends
• Ethan and Fiona are friends

We say that Alice, Bob, Cathy, and Danny are in Friend Group 1 (they are friends or have common friends). Ethan and Fiona are in Friend Group 2 (they are friends or have common friends).

In this task, we can easily tell the number of friend groups (there are 2 friend groups), as well as the size of the largest friend group (the largest group - Friend Group 1 - has 4 members).

This seems easy at first glance! We just need to "group them up". However, this is more complicated than you think. There are three potential solutions to this problem :

• Breadth-First Search (BFS)
• Depth-First Search (DFS)
• Union Find

We will learn different strategies for similar problems, and hopefully you know which one to use after learning the key concepts in graph theory.