Skip to main content

0261 - Graph Valid Tree (Medium)

https://leetcode.com/problems/graph-valid-tree/

Problem Statement​

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

Example 1:

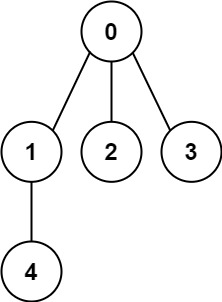
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

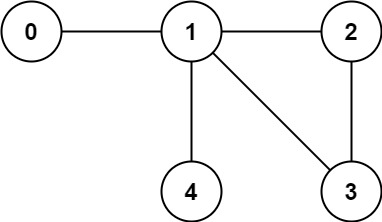
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

Constraints:

  • 1 <= n <= 2000
  • 0 <= edges.length <= 5000
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • There are no self-loops or repeated edges.

Approach 1: DSU​

If a graph is a valid tree, it must have exactly n - 1 edges. Besides, it cannot be fully connected and contain any cycles. Therefore, we just need check if there are n - 1 edges and any cycles. We can use DSU to check if element A and element B share the same parent. If so, it means that they are united, a cycle wound be there. Hence, we can return false immediately as a valid tree cannot have a cycle. Otherwise, we unite both element. If there is no cycle after iterating all elements, then we can simply check if there are n - 1 edges. There are other ways such as DFS and BFS to solve it.

Written by @wingkwong
class dsu {
 public:
  vector<int> root, rank;
  int n;
  int cnt;

  dsu(int _n) : n(_n) {
    root.resize(n);
    rank.resize(n);
    for(int i = 0; i < n; i++) {
        root[i] = i;
        rank[i] = 1;
    }
    cnt = n;
  }

  inline int getCount() { return cnt; }

  inline int get(int x) { return (x == root[x] ? x : (root[x] = get(root[x]))); }

  inline bool unite(int x, int y) {
    x = get(x);
    y = get(y);
    if (x != y) {
        if (rank[x] > rank[y]) {
            root[y] = x;
        } else if (rank[x] < rank[y]) {
            root[x] = y;
        } else {
            root[y] = x;
            rank[x] += 1;
        }
        cnt--;
      return true;
    }
    return false;
  }
};

class Solution {
public:
    bool validTree(int n, vector<vector<int>>& edges) {
        dsu d(n);
        for (auto x : edges) {
            if (!d.unite(x[0], x[1])) {
                return false;
            }
        }
        return (int) edges.size() == n - 1;
    }
};