0226 - Invert Binary Tree (Easy)

Problem Link

https://leetcode.com/problems/invert-binary-tree/

Problem Statement

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

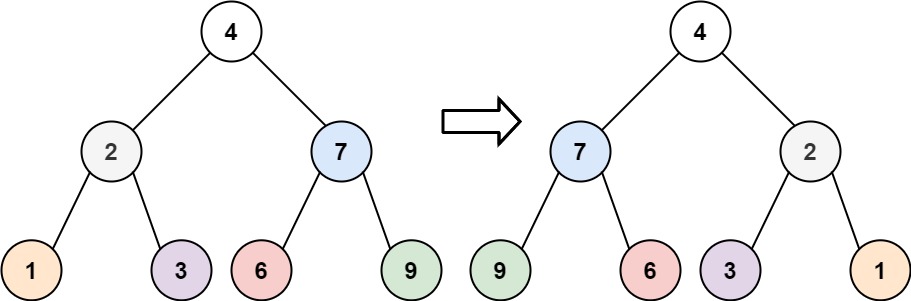
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:

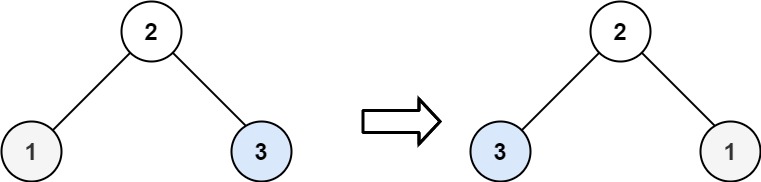
Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• 100 <= Node.val <= 100

Approach 1: Recursive Depth-First Search

Like many tree problems, they can often be solved with recursion, and this problem is no exception. When solving problems recursively it helps to think the problem through and think up the base case(s).

So looking at the problem, and the images, it appears that this problem is asking us to swap each child for each node. Then know that we can think about what happens if we reach the end, a node that has a value of null. That is our base case. If we reach a null node, we can just return the node.

Knowing that is our base case, all we are left with is understanding how to swap our children nodes. We can do that using a temporary variable to track the left child so we don't lose it. Setting the root node's left pointer to the right child, then setting the root node's right pointer to the temporary variable, which was our left child.

Simply that is it, then we can call our algorithm recursively on both the left and right children (or right to left, we will end up with the same answer), and finally return our root.

Time Complexity: $O(n)$ where n is the number of nodes in our binary tree, as we have to visit each node at least once.

Space Complexity: $O(n)$ for the size of our recursive call stack. Their will be $O(h)$ where h is the height of the tree function calls in our call stack, but in the worst case, ie a tree with only right child nodes, that will reach $O(n)$.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # Base case
        if not root:
            return root
        # Temp node so as not to lose the left child.
        tmp = root.left
        # set root's left pointer to the right child node.
        root.left = root.right
        # set root's right pointer to point at the tmp node, which is our left
        # child node.
        root.right = tmp
        # Note in python we could simplify the swapping as:
        # root.left, root.right = root.right, root.left
        # call our function recursively on both the left and right children.
        self.invertTree(root.left)
        self.invertTree(root.right)
        # return root node.
        return root

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    // base case
    if (!root) {
        return root;
    }
    // swap left and right nodes
    let tmp = root.left;
    root.left = root.right;
    root.right = tmp;
    // call function recursively on left and right nodes
    invertTree(root.left);
    invertTree(root.right);
    // return root node 
    return root;
};

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // base case
        if (!root) {
            return root;
        }
        // swap left and right node
        TreeNode* tmp = root->left;
        root->left = root->right;
        root->right = tmp;
        // call function recursively on left and right nodes
        invertTree(root->left);
        invertTree(root->right);
        // return root node
        return root;
    }
};

Approach 2: Iterative Depth-First Search

The iterative approach may be a little tricky if you've never seen it done before. To pull it off, we need a stack, and we can initialize it with our root node. Then while the stack contains values, we can pop them off the stack during each iteration. Similar to the recursive, during each iteration, all we have to do is swap our left and right child nodes, then add them to the stack to be processed themselves.

Time Complexity: $O(n)$ where n is the number of nodes in our binary tree, as we have to visit each node at least once.

Space Complexity: $O(n)$ for the size of the stack, as the size our stack reaches will be dependent on the number of nodes in the binary tree.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # Given null as a tree, return early.
        if not root:
            return root
        # Initialize our stack with the root node inside.
        stack = [root]
        # Iterate through each value in the stack.
        while stack:
            # pop the node off the end of the stack. O(1) time
            node = stack.pop()
            # Python we can swap left and right children simply like this:
            node.left, node.right = node.right, node.left
            # Check if the node has a child before adding it to the stack:
            # this makes error checking a lot easier, as we don't need to check
            # whether the node exists before swapping the left and right children
            # as we won't ever add the None nodes to the stack.
            if node.left:
                stack.append(node.left)
            # repeat for right child
            if node.right:
                stack.append(node.right)
        # return root node.
        return root

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    // base case
    if (!root) {
        return root;
    }
    // initialize stack and add root inside
    stack = [];
    stack.push(root);
    // go through every value in stack
    while (stack.length) {
        // pop the last node from the stack
        let node = stack.pop();
        if (node != null) {
            // swap left and right nodes
            let tmp = node.left;
            node.left = node.right;
            node.right = tmp;
            // add left and right nodes in stack
            stack.push(node.left, node.right);
        } 
    }
    // return root node 
    return root;
};

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // base case 
        if (!root) {
            return root;
        }
        // initialize stack and add root inside 
        stack<TreeNode*> st;
        st.push(root);
        // go through every value in stack
        while (!st.empty()) {
            // pop the last node from the stack
            TreeNode* node = st.top();
            st.pop();
            // if node exist
            if (node != NULL) {
                // swap left and right nodes
                TreeNode* tmp = node->left;
                node->left = node->right;
                node->right = tmp;
                // insert left and right nodes in stack
                st.push(node->left);
                st.push(node->right);
            }
        }
        // return root node
        return root;
    }
};

Approach 3: Iterative Breadth-First Search

Similarly, in most cases where you can do an iterative DFS, you can also do an iterative BFS using a queue. It will be the same idea as iterative DFS, just using a queue, meaning we will add nodes to the right side of our queue and pop them off the left side of our queue instead.

Time Complexity: $O(n)$ where n is the number of nodes in our binary tree, as we have to visit each node at least once.

Space Complexity: $O(n)$ for the size of the queue. In the worst case we will have a full level of nodes inside our queue, which in a full tree, the last level will contain $\frac {n}{2}$ nodes, which for our case means $O(n)$ space.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # Given None as a root node, we can return early.
        if not root:
            return root
        # initialize our our queue with root node as our first value.
        q = deque([root])
        while q:
            # pop root node off the left side of our queue.
            node = q.popleft()
            # swap the children nodes.
            node.left, node.right = node.right, node.left
            # only add the node to the q's right side, if the node exists.
            if node.left:
                q.append(node.left)
            # same for the right node.
            if node.right:
                q.append(node.right)
        # return the root.
        return root

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        // base case
        if (!root) {
            return root;
        }
        // inititalize queue
        queue<TreeNode*> q;
        // insert root inside queue
        q.push(root);
        // go through all values in queue
        while (!q.empty()) {
            // pop the front node from queue
            TreeNode* node = q.front();
            q.pop();
            // if node exist
            if (node != NULL) {
                // swap left and right nodes
                TreeNode* tmp = node->left;
                node->left = node->right;
                node->right = tmp;
                // insert left and right nodes in queue
                q.push(node->left);
                q.push(node->right);
            }
        }
        // return root node
        return root;
    }
};

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var invertTree = function(root) {
    // base case
    if (!root) {
        return root;
    }
    // initialize queue and insert root inside queue
    let q = new Queue();
    q.enqueue(root);
    // go through all elements in queue
    while (!q.isEmpty()) {
        // pop the front node from queue
        let node = q.dequeue();
        // if node exist
        if (node) {
            // swap left and right nodes
            let tmp = node.left;
            node.left = node.right;
            node.right = tmp;
            // insert left and right nodes in queue
            q.enqueue(node.left);
            q.enqueue(node.right);
        }
    }
    // return root node
    return root;
};