0297 - Serialize and Deserialize Binary Tree (Hard)
Problem Link
https://leetcode.com/problems/serialize-and-deserialize-binary-tree/
Problem Statement
Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
Example 1:
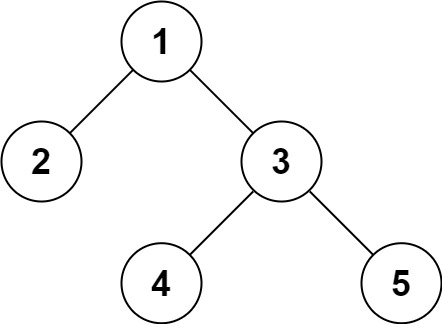
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]
Example 2:
Input: root = []
Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 10^4]. -1000 <= Node.val <= 1000
Approach 1: Breadth-First Search
We can use a queue/BFS to order our nodes in a level order traversal. That means looping through level by level and appending them to a string or an array. Note for Python, and potentially any other languages that use immutable strings, we will use an array first, then convert our serialized array into a string after like the question asks. Python we can use .join method (This prevents remaking the string during each concatenation). We will also need to separate our nodes in the string with a separator, and use a character to denote a null node.
Serializing: Time Complexity: . We must read each node, and then convert it to a serialized form. We can't skip nodes.
Space Complexity: . Our queue to perform BFS will have nodes in the last layer, and if we use an array to serialize before we convert to a string, the array will have elements.
The tricky part then becomes deserializing. To deserialize we must read our input string and determine what a node will be (values between our separators), then we will need ways to determine which node is which child, and whether it is the left or right child. (In Python we can simplify this using our array.split(), otherwise we would need to track start and end points of the string, then splice the string around those start and end points to get the values.)
Again we can use a queue to solve which node is child of which. By appending all nodes to the queue and using a boolean to determine whether the next node being read in is the left or right child. If it is the right child, we can then pop the node out of the queue, and start adding children to the new node in front of the queue.
Deserializing: Time Complexity: . We must process each node.
Space Complexity: , We must create nodes, and we will also need up to space for our queue, and potentially more if we convert our string to an array first.
- Python
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Codec:
def serialize(self, root):
"""Encodes a tree to a single string.
:type root: TreeNode
:rtype: str
Time: O(n)
- process each node
- O(n) ''.join(arr) at the end.
Space: O(n)
- queue up to n space.
- array to hold our values will need n space.
"""
# create empty array to hold our values
arr = []
# initialize our queue with our root node.
q = deque([root])
# while our queue has values,
while q:
# loop through current level.
for n in range(len(q)):
# pop left most node in queue
node = q.popleft()
# if node is not a null node
if node:
# add nodes value as a string to our array.
arr.append(str(node.val))
# add the left and right children.
q.append(node.left)
q.append(node.right)
else:
# null node -> add a null value, we will use 'X'. Could
# use anything as long as it isn't our spacing character
# or a number value.
arr.append('X')
# question asks for it as a string, convert to a string at the end to
# to only do O(n) work. If we used a string instead of an array, string
# concatenation would mean we'd have to recreate the string each step.
return "#".join(arr)
def deserialize(self, data):
"""Decodes your encoded data to tree.
:type data: str
:rtype: TreeNode
Time: O(n)
- process each node
- O(n) to split our string into an array for easier traversal.
Space: O(n)
- recreate our tree with n nodes.
- array will take up n space.
- queue will take up to n space.
"""
# Base Case
if data == 'X':
return None
# Turn our encoded string into an array of values. We do it this way
# to simplify the reading of the data.
arr = data.split('#')
# Create root using first value in tree
root = TreeNode(int(arr[0]))
# create q, used to help add children
q = deque([root])
# boolean to tell us whether the child is left or right child.
right = False
# loop through all the nodes, except first which we already made.
for i in range(1, len(arr)):
# get the value, maybe a null node.
val = arr[i]
# null node, which we said was 'X'
if val == 'X':
# set the node to be None
node = None
else:
# not a null node, create the tree node, add it to the queue.
node = TreeNode(int(val))
# since it is in the queue, it will receive children later.
q.append(node)
#Handle Children
# if right == true, it means next child is first value in the queue's
# right child.
if right:
# set current node to be the right child
q[0].right = node
# pop the node, since it no longer needs children
q.popleft()
# set right to false as the next node first child will be a
# left child.
right = False
# right == false, next child is the first value in the queue's left
# child.
else:
# set current node to be the left child
q[0].left = node
# update right variable, to denote we need to set right child
# on the next iteration.
right = True
# Finally we can return the root of our tree.
return root