0230 - Kth Smallest Element in a BST (Medium)

Problem Link

https://leetcode.com/problems/kth-smallest-element-in-a-bst/

Problem Statement

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:

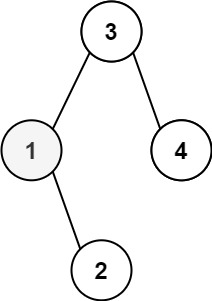
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:

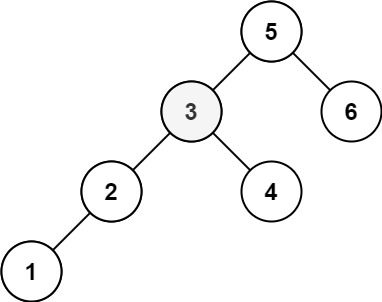
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

• The number of nodes in the tree is n.
• 1 <= k <= n <= 10^4
• 0 <= Node.val <= 10^4

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

Approach 1: Recursive Inorder Traversal

If you know your tree traversals, specifically inorder traversal, and you understand the layouts of a binary search tree. Then that means you know the inorder traversal of a BST will give us the node values in sorted order. Knowing that we can simply generate the inorder traversal of the tree, and return the kth element.

Time Complexity: $O(n)$, must traverse each node to create the inorder traversal array.

Space Complexity: $O(n)$, to store the values of each node inside an array and utilize recursive call stack.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorder(self, root) -> [int]:
        # initialite array
        arr = []
        # if root is not a null node.
        if root:
            # recursively call on left side, adding output to arr.
            arr += self.inorder(root.left)
            # add the current value to arr
            arr.append(root.val)
            # recursively call on right side, adding output to arr.
            arr += self.inorder(root.right)
        # return the array.
        return arr

    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        # get the inorder traversal array.
        inorder = self.inorder(root)
        # return k-1 value since questions wants kth smallest, 1-indexed
        return inorder[k-1]

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    // initialize array
    vector<int> res;
    // recursive function
    void inorder(TreeNode* root) {
        // if root exist
        if (root != NULL) {
            // recursive call on the left side
            inorder(root->left);
            // insert current node to result array
            res.push_back(root->val);
            // recursive call on the right side
            inorder(root->right);
        }
    }

    int kthSmallest(TreeNode* root, int k) {
        // get inorder traversal array
        inorder(root);
        // return kth smallest value
        return res[k - 1];
    }
};

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */

// recursive function
const inorder = function(root) {
    // if root exist 
    if (root !== null) {
        // recursive call on the left side
        inorder(root.left);
        // insert current node to result array
        res.push(root.val);
        // recursive call on the right side
        inorder(root.right);
    }
}

var kthSmallest = function(root, k) {
    // initialize result array
    res = [];
    // get inorder traversal array
    inorder(root);
    // return kth smallest value
    return res[k - 1];
};

Approach 2: Iterative Inorder Traversal

We can also do our inorder traversal iteratively. This time, when we reach our answer, we can exit as soon as we find it, and save on space as we don't need to completely iterate over the whole tree, just until we reach the kth smallest.

If you've never seen inorder traversal done iteratively before, we need both a stack and a variable to track the current node. Then we use 2 while loops, one while the stack and the current node exists.

The second loop goes inside the first, and tracks the current node, adding the current node to the stack, so we can backtrack in the future, then we move our node pointer to the left.

When we finally reach a null node, we then need to pop a node off the stack, process the node then move the node pointer right.

Time Complexity: $O(h+k)$ where $h$ is the height of the tree, and $k$ is given. We will have to traverse down the tree to the lowest value node, then traverse back up k times to reach the kth. Given a skewed tree, this could be $O(n+k)$

Space Complexity: $O(h)$ where $h$ is the height of the tree to maintain our stack. In the worst case $h == n$ with a skewed trees.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        # initialize a current node pointer
        node = root
        # initialize stack for backtracking purposes
        stack = []
        # initialize an n counter to count up to k.
        n = 0
        # while our current node exists or the stack has values:
        while node or stack:
            # while our current node exists:
            while node:
                # add current node to the stack for backtracking
                stack.append(node)
                # move our current node pointer to the left child.
                node = node.left
            # Done going left, now we process the node and go right.
            # node will equal null either from the above loop, or below process. 
            # So we need to pop a new node off the stack.
            node = stack.pop()
            # Update our n variable.
            n += 1
            # Check that n == k: if so we found the kth smallest.
            if n == k:
                # return the kth smallest value
                return node.val
            # Done the above process, we can move the current node pointer right.
            # Note: if we reach a null node, the while loop will still run
            # as long as values are inside the stack, which will backtrack us
            # to the next node.
            node = node.right

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function(root, k) {
    // initialize variable to count up to k
    let n = 0;
    // initialize stack
    let stack = [];
    // initialize curr node pointer
    let curr = root;
    // while current node is not null and stack is not empty
    while (curr || stack) {
        // while current node is not null 
        while (curr) {
            // add current node to the stack
            stack.push(curr);
            // shift current pointer to the left
            curr = curr.left;
        }
        // current pointer is done going left
        // pop that current node from the stack  
        curr = stack.pop();
        // update count variable
        n++;
        // if we found kth smallest element
        if (n === k) {
            // return kth smallest value
            return curr.val;
        }
        // shift current pointer to the right 
        curr = curr.right;
    }
};

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        // initialize stack
        stack<TreeNode*> st;
        // initialize variable to count up to k
        int n = 0;
        // initialize current node pointer
        TreeNode* curr = root;
        // while current node is not NULL and stack is not empty
        while (curr || st.size()) {
            // while current node is not NULL
            while (curr) {
                // add current node to the stacl
                st.push(curr);
                // shift current pointer to the left
                curr = curr->left;
            }
            // current pointer is done going left
            // pop that current node from the stack 
            curr = st.top();
            st.pop();
            // update count variable  
            n++;
            // if we found kth smallest element
            if (n == k) {
                // return kth smallest element
                return curr->val;
            }
            // shift current pointer to the right
            curr = curr->right;
        }
        // kth smallest not found so return -1 
        return -1;
    }
};