0623 - Add One Row to Tree (Medium)

Problem Link

https://leetcode.com/problems/add-one-row-to-tree/

Problem Statement

Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.

Note that the root node is at depth 1.

The adding rule is:

• Given the integer depth, for each not null tree node cur at the depth depth - 1, create two tree nodes with value val as cur's left subtree root and right subtree root.
• cur's original left subtree should be the left subtree of the new left subtree root.
• cur's original right subtree should be the right subtree of the new right subtree root.
• If depth == 1 that means there is no depth depth - 1 at all, then create a tree node with value val as the new root of the whole original tree, and the original tree is the new root's left subtree.

Example 1:

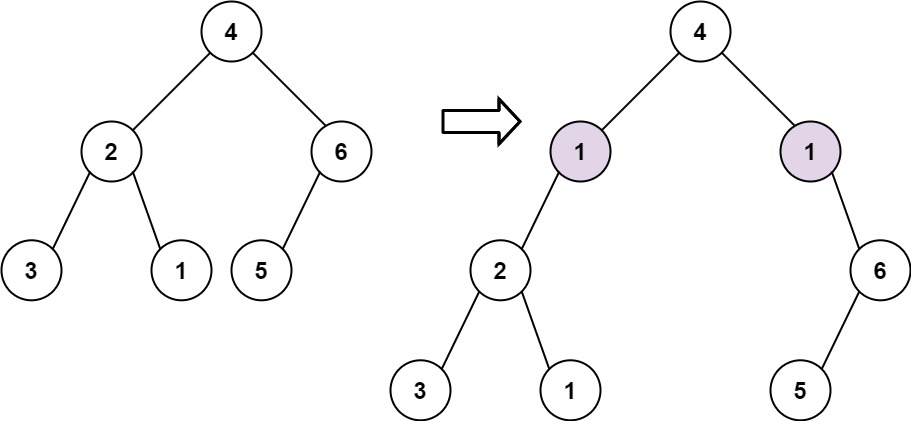
Input: root = [4,2,6,3,1,5], val = 1, depth = 2
Output: [4,1,1,2,null,null,6,3,1,5]

Example 2:

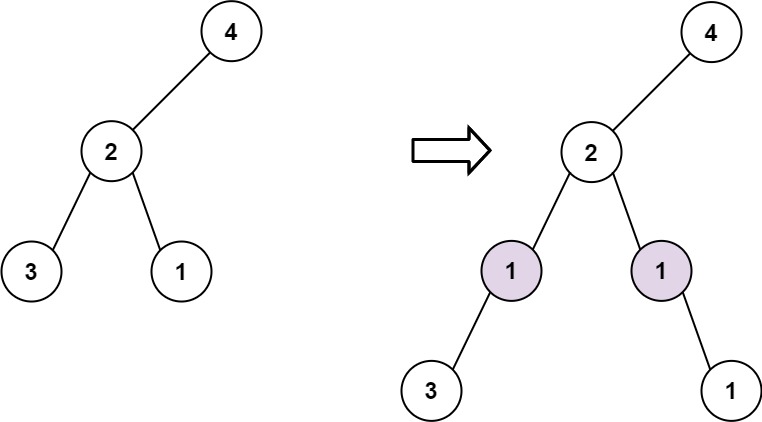
Input: root = [4,2,null,3,1], val = 1, depth = 3
Output: [4,2,null,1,1,3,null,null,1]

Constraints:

• The number of nodes in the tree is in the range [1, 10^4].
• The depth of the tree is in the range [1, 10^4].
• -100 <= Node.val <= 100
• -10^5 <= val <= 10^5
• 1 <= depth <= the depth of tree + 1

Approach 1: Recursion (DFS)

This approach uses a simple DFS approach. The recursive function $insert(node, currDepth, val, depth)$ can be used to recursively reach a node where we need to insert two nodes.

The parameters used in the function are:

• $node$: the current node on which DFS is called upon
• $currDepth$: the depth of current node $node$
• $val$: value of nodes to be inserted
• $depth$: the depth at which nodes are to be inserted

Note: the parameters $val$ and $depth$ never change during program execution and hence can be made global

Now, whenever we reach a node with depth $depth-1$ we create two new nodes $l$ and $r$ and link $l$'s and $r$'s left and right children to be $node$'s left and right children respectively, and then we re-assign $node$'s left and right children as $l$ and $r$ respectively.

If $node$ is at a depth < $depth$ we recursively call $insert$ for $node$->$right$ and $node$->$left$ with increased depths.

One special case to be taken care of is when $depth$ is 1 because here the original root of tree is changed so we create a new node, assign this new node's left child as root and return this new node as root of tree.

Time Complexity: $O(n)$. A total of n nodes of the given tree will be considered in worst case.

Space Complexity: $O(n)$. The depth of the recursion tree can go upto n in the worst case (skewed tree).

C++

Written by @divyansh_0602

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void insert(TreeNode *node, int currDepth, int val, int depth) {
        if (!node) return;

        // if we reach the node where we need to create two nodes
        if (currDepth == depth - 1) {
            // create two new nodes
            TreeNode *l = new TreeNode(val);
            TreeNode *r = new TreeNode(val);

            // link the new nodes
            l->left = node->left;
            r->right = node->right;

            // change original links
            node->left = l;
            node->right = r;

            // return since we do not need to further deep in the tree
            return;
        }

        // if we do not reach desired depth, go deep in the tree
        insert(node->left, currDepth + 1, val, depth);
        insert(node->right, currDepth + 1, val, depth);
    }

    TreeNode *addOneRow(TreeNode *root, int val, int depth) {
        // since root is changed in this case, handle this case seperately
        if (depth == 1) {
            TreeNode *newNode = new TreeNode(val);
            newNode->left = root;
            return newNode;
        }
        // recursive function for insertion of new nodes
        insert(root, 1, val, depth);
        return root;
    }
};

Elixir

Written by @jit

@spec add_one_row(root :: TreeNode.t | nil, val :: integer, depth :: integer) :: TreeNode.t | nil
# A basic DFS implementation:
def add_one_row(nil, _val, _), do: nil
def add_one_row(root, val, 1), do: %TreeNode{val: val, left: root}

def add_one_row(root, val, 2) do
  %{root |
    left:  %TreeNode{val: val, left: root.left},
    right: %TreeNode{val: val, right: root.right}
  }
end

def add_one_row(root, val, d) do
  %{root |
    left:  add_one_row(root.left, val, d - 1),
    right: add_one_row(root.right, val, d - 1)
  }
end

Approach 2: Iterative DFS

• Time complexity: $O(n)$ where $n$ is the number of nodes.
• Space complexity: $O(h)$ where $h$ is the height of the tree that can vary depending how balanced / unbalanced to tree is from $O(\log n)$ to $O(n)$.

C++

Written by @heder

static TreeNode* addOneRow(TreeNode* root, int val, int depth) {
    if (depth == 1) return new TreeNode(val, root, nullptr);
    
    stack<pair<TreeNode*, int>> st;
    st.push({root, depth - 1});
    
    while (!empty(st)) {
        auto [node, depth] = st.top(); st.pop();
        
        if (depth == 1) {
            node->left = new TreeNode(val, node->left, nullptr);
            node->right = new TreeNode(val, nullptr, node->right);
            continue;
        }
        
        if (node->left) st.push({node->left, depth - 1});
        if (node->right) st.push({node->right, depth - 1});
    }

    return root;
}

Approach 3: Level order traversal / iterative

• Time complexity: $O(n)$ we might need to visit all the nodes.
• Space Complexity: Worst case we have $\approx n/2$ nodes in the queue, hence the space complexity is $O(n)$

C++

Written by @heder

static TreeNode* addOneRow(TreeNode* root, int val, int depth) {
    if (depth == 1) return new TreeNode(val, root, nullptr);

    queue<TreeNode*> q;
    q.push(root);
    for (int i = 1; i < depth; ++i) {
        int q_size = size(q);
        while (q_size--) {
            TreeNode* node = q.front(); q.pop();
            
            if (i == depth - 1) {
                node->left = new TreeNode(val, node->left, nullptr);
                node->right = new TreeNode(val, nullptr, node->right);
            } else {
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }
    }
    
    return root;
}

A variant could be to do the level order traversal to $depth - 1$ and then insert the new nodes, like this:

C++

Written by @heder

 static TreeNode* addOneRow(TreeNode* root, int val, int depth) {
    if (depth == 1) return new TreeNode(val, root, nullptr);

    queue<TreeNode*> q;
    q.push(root);
    for (int i = 1; i < depth - 1; ++i) {
        int q_size = size(q);
        while (q_size--) {
            TreeNode* node = q.front(); q.pop();
            
            if (node->left) q.push(node->left);
            if (node->right) q.push(node->right);
        }
    }

    while (!empty(q)) {
        TreeNode* node = q.front(); q.pop();
        node->left = new TreeNode(val, node->left, nullptr);
        node->right = new TreeNode(val, nullptr, node->right);
    }
    
    return root;
}