0684 - Redundant Connection (Medium)

Problem Link

https://leetcode.com/problems/redundant-connection/

Problem Statement

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

Example 1:

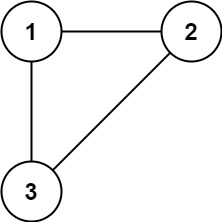
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

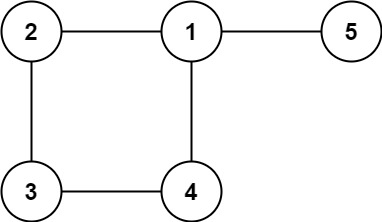
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

Constraints:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• There are no repeated edges.
• The given graph is connected.

Approach 1: Union Find

We can create $n$ graphs of size 1, and combine the graphs based on each edge given in edges. To do this we would need to track the parent nodes of each node, which can be done in an array where the index is the node, and the value is the index of the node's parent. We can similarily track the size of each graph using an array, where the index of the array is the node, and the value is the size of the graph.

Then for each edge in edges we can combine those graphs which share an edge. We do that by finding the root of each graph, using a $find()$ algorithm, and then combining the smaller graph with the larger graph. If we ever run into an edge that combines two nodes that are already connected, we know that this edge would cause a cycle, and be the edge we would want to remove.

Time Complexity: $O(n)$, where n is the number of edges. It ends up being about $O(n*α(n))$ where $α(n)$ is the inverse Ackerman function, which for our worst case, will only ever be a constant, and $n$ will be the number of calls to our $find()$ algorithm.

Space Complexity: $O(n)$ to maintain our $parent$ and $rank$ arrays.

Python

Written by @ColeB2

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        # initialize parent, and rank
        # The index of each value is the node number, the value is
        # the index of the nodes parent.
        # Initialize it so each node is it's own parent.
        parent = [i for i in range(len(edges) + 1)]
        # Size of each 'graph\tree'. Starting out each graph will be
        # a graph of its own self, so initialize all as size 1.
        rank = [1] * (len(edges) + 1)
        # Find algorithm, finds' the parent given a node.
        def find(n):
            # Initialize node to be the parent of n.
            node = parent[n]
            # while node isn't it's own parent
            # Walk up the nodes graph of ancestors until we reach the root.
            while node != parent[node]:
                # Path Compression: update the parent of current node to be
                # parent of the parent to make subsequent find on node faster.
                parent[node] = parent[parent[node]]
                node = parent[node]
            # node which is the root.
            return node
        # Union algorithm: Combines the graphs of n1 and n2.
        def union(n1, n2):
            # find roots of both n1 and n2.
            p1, p2 = find(n1), find(n2)
            # if roots of both n1, n2 are equal, it means both
            # nodes are already in the same graph.
            if p1 == p2:
                return False
            # p1 is part of the bigger graph:
            if rank[p1] > rank[p2]:
                # Change p2 parent to be p1
                parent[p2] = p1
                # update p1 graph size with additional values of p2.
                rank[p1] += rank[p2]
            else:
                # p2 is the bigger/equal size graph
                # set p1 parent to be p2
                parent[p1] = p2
                # update size of graph of p2.
                rank[p2] += rank[p1]
            # Graphs are joined, return True.
            return True
        # Loop each each in edges
        for n1, n2 in edges:
            # union of both edges returns false, it means both
            # edges were already apart of the same graph, so 
            # the next edge would cause a cycle. So we would return
            # that edge.
            if not union(n1, n2):
                return [n1, n2]
            # Otherwise continue looping through the edges.