Skip to main content

0695 - Max Area of Island (Medium)

https://leetcode.com/problems/max-area-of-island/

Problem Statement​

You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.

The area of an island is the number of cells with a value 1 in the island.

Return the maximum area of an island in grid. If there is no island, return 0.

Example 1:

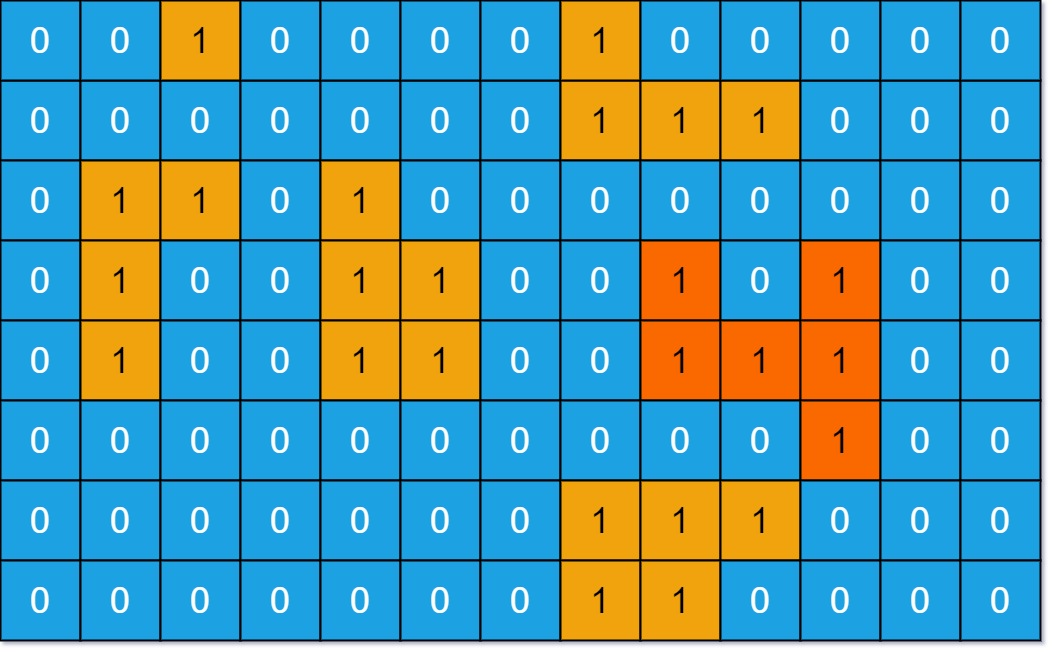
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.

Example 2:

Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0

Constraints:

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 50
  • grid[i][j] is either 0 or 1.

We can traverse the grid, and when we find an island, run our BFS on the island. For every 11 we find we can increment our area counter, as well as update a global max area variable.

Time Complexity: O(m∗n)O(m * n) must traverse each cell in the grid.

Space Complexity: O(m∗n)O(m * n). For the size of our queue.

Written by @ColeB2
class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        # intiialize rows, cols, and a global max area to track
        # the size of the largest island.
        ROWS, COLS = len(grid), len(grid[0])
        self.max_area = 0
        # BFS function, takes to parameters, row, r and column, c.
        def bfs(r, c):
            # initialize our queue with current row, r and column, c
            q = deque([(r,c)])
            # initialize area starting at 0.
            area = 0

            while q:
                # pop row and col off the queue
                row, col = q.popleft()
                # check that it is inbounds, and a 1/land
                if (row < 0 or row >= ROWS
                    or col < 0 or col >= COLS
                    or grid[row][col] != 1
                    ):
                    continue
                # It is in bounds and land, we will mark it as visited
                # we can re-use the grid by just setting the spot to -1.
                grid[row][col] = -1
                # update our area and global max area.
                area += 1
                self.max_area = max(area, self.max_area)
                # loop through 4 adjacent directions
                for dr, dc in ((1,0), (0,1), (-1,0), (0, -1)):
                    # add 4 adjacent cells to our queue.
                    q.append((row + dr, col + dc))
        # Loop through our board
        for r in range(ROWS):
            for c in range(COLS):
                # find land, run bfs at that position
                if grid[r][c] == 1:
                    bfs(r, c)
        return self.max_area

For each land, we can run DFS to calculate the area of the current island. We set the visited cell to other value so that it won't re-calculate. Get the maximum area and return it.

Time Complexity: O(m∗n)O(m * n) must traverse each cell in the grid.

Space Complexity: O(m∗n)O(m * n).

Written by @wingkwong
class Solution {
public:
    int ans = 0;
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        for(int i = 0; i < grid.size(); i++) {
            for(int j = 0; j < grid[0].size(); j++) {
                if(grid[i][j] == 1) {
                    // if it is 1, then we can start from this cell
                    ans = max(ans, dfs(grid, i, j));
                }
            }
        }
        return ans;
    }
    
    int dfs(vector<vector<int>>& grid, int i, int j) {
        // if it is 0 or out of bound, return 0
        if(i < 0 || j < 0 || i > grid.size() - 1 || j > grid[0].size() - 1 || grid[i][j] != 1) return 0;
        // set it to 0 so that we won't visit it again
        grid[i][j] = 0;
        // 1 (current cell) + the result from four directions
        return 1 +
            dfs(grid, i + 1, j) +
            dfs(grid, i, j + 1) +
            dfs(grid, i - 1, j) +
            dfs(grid, i, j - 1);
    }
};