0662 - Maximum Width of Binary Tree (Medium)

Problem Link

https://leetcode.com/problems/maximum-width-of-binary-tree/

Problem Statement

Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.

It is guaranteed that the answer will in the range of 32-bit signed integer.

Example 1:

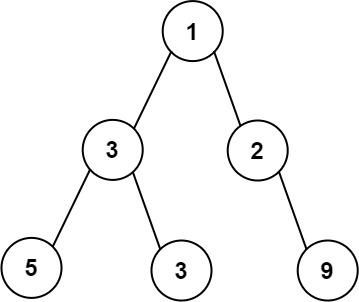
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).

Example 2:

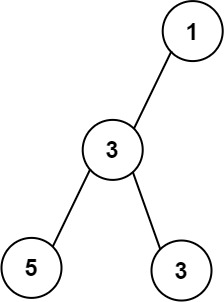
Input: root = [1,3,null,5,3]
Output: 2
Explanation: The maximum width existing in the third level with the length 2 (5,3).

Example 3:

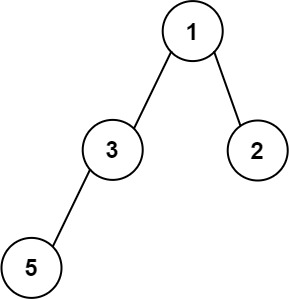
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width existing in the second level with the length 2 (3,2).

Constraints:

• The number of nodes in the tree is in the range [1, 3000].
• -100 <= Node.val <= 100

Approach 1: BFS

We want to traverse each node level by level to calculate the width between the leftmost and the rightmost non-null nodes on the same level. We can use queue to perform BFS.

First we initialise a queue with a pair of tuple $(node, idx)$. Then we append the root with idx $0$ at the beginning. How do we assign $idx$ for other nodes? Given a full binary tree, we can easily see a pattern here. If a node with idx $i$ has the left node, the its idx would be $2 * i$. If a node with idx $i$ has the right node, the its idx would be $2 * i + 1$.

For each level, we calculate the width between the leftmost and rightmost nodes, which are the first element $l$ in the queue and the last element $r$ in the queue respectively, and check if it could be maximum value. The width between those two nodes is simply $r_{idx} - l_{idx} + 1$. For example, on the last level, the width between the leftmost node and the rightmost node would be $7 - 4 + 1 = 4$.

For each element in the queue, we check if it has the left node or the right node. If so, we add it to the queue for further processing. We return the answer after we process all the nodes.

Written by @wingkwong

class Solution {
public:
    using ll = long long;
    int widthOfBinaryTree(TreeNode* root) {
        int ans = 0;
        queue<pair<TreeNode*, int>> d; // <node, idx>
        // push the first element with idx = 0
        d.push({root, 0});
        // BFS
        while (!d.empty()) {
            // l_idx is the idx of the leftmost node
            // r_idx is the idx of the rightmost node
            ll l_idx = d.front().second, r_idx = d.back().second;
            // define n here outside as d.size() may be changed
            int n = (int) d.size();
            // iterate each tuple
            for (int i = 0; i < n; i++) {
                // get one tuple and pop it
                auto x = d.front(); d.pop();
                // get the idx of the current node
                auto idx = x.second ;
                // if it has the left node, push it for the next level
                // with idx = 2 * cur_idx
                if (x.first->left)  d.push({x.first->left, (ll) 2 * idx});
                // if it has the right node, push it for the next level
                // with idx = 2 * cur_idx + 1
                if (x.first->right) d.push({x.first->right, (ll) 2 * idx + 1});
            }
            // check if the current level got the max width
            ans = max(ans, int(r_idx - l_idx + 1));
        }
        return ans;
    }
};