0994 - Rotting Oranges (Medium)

Problem Link

https://leetcode.com/problems/rotting-oranges/

Problem Statement

You are given an m x n grid where each cell can have one of three values:

• 0 representing an empty cell,
• 1 representing a fresh orange, or
• 2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

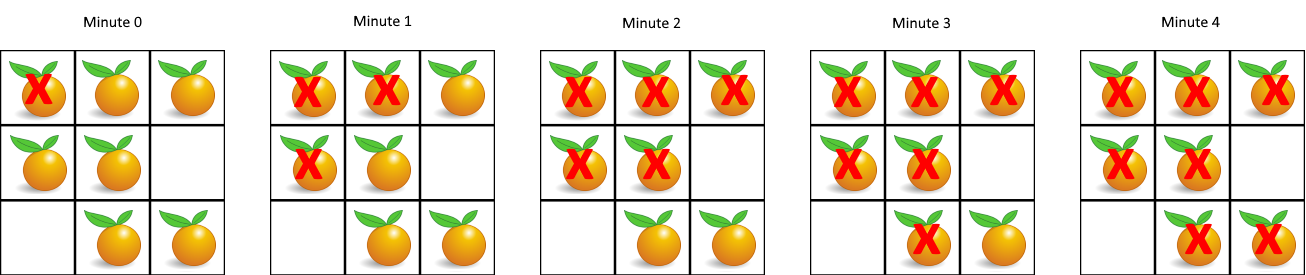
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] is 0, 1, or 2.

Approach 1: Breadth-First Search

Since we must track time, a breadth-first search approach makes the most sense, as we can track each iteration of our bfs loop, and update the time before moving on to the next.

First, we need to iterate our grid looking for rotten oranges to add to our queue. Note, if we also take the time during this iteration to count the number of fresh oranges, we can save a little time in the end.

Once we have a queue of oranges, we just need to run our BFS and update our time after we exhaust all current cells in each iteration of it, and finally return the time as long as we have successfully converted all fresh oranges to rotten ones.

Time Complexity: $O(m * n)$ where m is the number of rows, and n is the number of columns. We must traverse the graph once to find all our fresh/rotten oranges, and then potentially again during our BFS.

Space Complexity: $O(m * n)$. In the worst case, all oranges will be rotten, and our queue will be of size $m * n$.

Python

Written by @ColeB2

class Solution:
    def orangesRotting(self, grid: List[List[int]]) -> int:
        # Track number of rows and cols
        ROWS, COLS = len(grid), len(grid[0])
        # initialize our queue, and number of fresh oranges in the grid.
        q = deque([])
        fresh = 0
        # iterate the grid
        for r in range(ROWS):
            for c in range(COLS):
                # fresh oranges, increment our fresh count
                if grid[r][c] == 1:
                    fresh += 1
                # rotten oranges can be added to the queue.
                if grid[r][c] == 2:
                    q.append((r, c))
        # initialize our time, and directions for our BFS.
        time = 0
        dirs = ((1, 0), (0, 1), (-1, 0), (0, -1))
        # while we have a queue of rotten oranges, and fresh still remaining.
        while q and fresh > 0:
            # loop through all the rotten oranges currently in the queue.
            for _ in range(len(q)):
                # get their position in the grid
                row, col = q.popleft()
                # check the 4 adjacent oranges
                for (dr, dc) in dirs:
                    # the position of the adjacent oranges.
                    r, c = row + dr, col + dc
                    # check the adjacent oranges are in bounds and fresh.
                    if (r < 0 or r >= ROWS
                        or c < 0 or c >= COLS
                        or grid[r][c] != 1
                        ):
                        continue
                    # They are fresh, make them rotten, 
                    grid[r][c] = 2
                    fresh -= 1
                    # add new rotten orange to the queue. We won't reach
                    # it on this iteration, as we are only iterating
                    # through the rotten from the last iteration.
                    q.append((r, c))
            # Since we only looped through the rotten oranges inside the
            # queue, and not the adjacent ones, we can increment the time
            # now, and on the next iteration we will check those adjacent ones.
            time += 1
        # If we turned all oranges rotten, return the time, else -1.
        return time if fresh == 0 else -1