Merge Sort

Author: @Sreetama2001

Contributor: @wingkwong

Overview

Merge Sort works by recursively breaking down an array into multiple subarrays and then after comparing each of the subarrays. It arranges them into ascending or descending order by value and merges them into a single sorted array.

Suppose we have an array of integers $[6, 5, 3, 1, 8, 7, 2, 4]$.

In Python it is called list and in C++ it can be called either array or vector and in Java it is called a ArrayList.

Then we can see that merge sort is performed in this way.

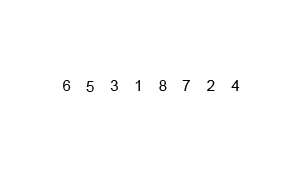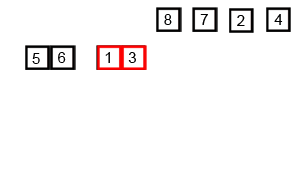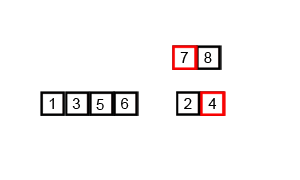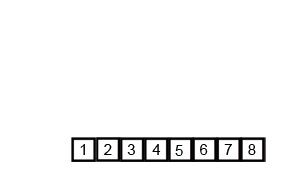
Image by Brian Hans via Medium

Algorithm

Divide

• Calculate the midpoint by checking if the left index is less than the right index, if yes divide the array.
• Now continue dividing the array until $index_{left} < index_{right}$ becomes false, that is until the division is not possible.

Conquer

• After dividing the array into the smallest units, start merging the elements again by comparing them.
• We need to compare and merge starting from the last splits or last smallest units. So Recursion needs to be done here.

Merge

• Since each half is already sorted so we need to just sort between 2 halves to combine / merge than to make a bigger sorted array.

Example: 0912 - Sort an Array

Given an array of integers nums, sort the array in ascending order and return it. You must solve the problem without using any built-in functions in O(nlog(n)) time complexity and with the smallest space complexity possible.

Top Down Approach

Algorithm

• if $left == right$
  • array has only one element, hence return.
• if $right > left$
  • find the middle point to divide the array into two halves: $middle = left + (right - left) / 2$
  • call mergeSort again for first half for further dividing: call $mergeSort(array, left, middle)$
  • call mergeSort again for second half for further dividing: call $mergeSort(array, middle + 1, right)$
  • merge the two halves sorted: call $merge(array, left, middle, right)$
  • merge function is called to compare and merge the elements into an array

C++

class Solution {
public:
    void merge(vector<int>& nums, int l, int m, int r) {
        // create a temporary array
        vector<int> tmp(r - l + 1);
        // index for left subarray 
        int i = l;
        // index for right subarray 
        int j = m + 1; 
        // index for temporary array
        int k = 0; 
        while (i <= m && j <= r) {
            // increment the left pointer 
            // if the right pointer element is bigger 
            // Since we are sorting in ascending order,left(smaller element) goes first
            if(nums[i] <= nums[j]) tmp[k++] = nums[i++];   
            else tmp[k++] = nums[j++];
        }
        // Since in the above while loop if one condition stop satisfying loop breaks 
        // Then we need to take care of  next / remaining  elements  
        // Hence adding remaining elements of left half
        while (i <= m) tmp[k++] = nums[i++];
        // adding remaining elements of right half
        while (j <= r) tmp[k++] = nums[j++]; 
        // Copy data to nums
        for (i = 0; i < k; i++) nums[l + i] = tmp[i];
    }

    void mergeSort(vector<int>& nums, int l, int r) {
        if (l >= r) return;
        // middle index, same as (l + r) / 2
        int m = l + (r - l) / 2;
        mergeSort(nums, l, m);
        mergeSort(nums, m + 1, r);
        merge(nums, l, m, r);
    }

    // function to return sorted array in leetcode
    vector<int> sortArray(vector<int>& nums) {
        mergeSort(nums, 0, nums.size() - 1);
        return nums;
    }
};

Python3

class Solution:

    def sortArray(self, nums: List[int]) -> List[int]:
        self.merge_Sort(nums)
        return nums
    
    def merge_Sort(self,nums: List[int]) -> List[int]:
       if len(nums) > 1:
           # calculate the middle to divide by mid 
           mid = len(nums) // 2  
           leftArray = nums[:mid]  
           rightArray = nums[mid:]  

           self.merge_Sort(leftArray)
           self.merge_Sort(rightArray)

           i = j = k = 0

           while i < len(leftArray) and j < len(rightArray): 
               if leftArray[i] < rightArray[j]:
                   # smaller element is merged first
                   # remember we are sorting in ascending order  
                   nums[k] = leftArray[i] 
                   # incrementing the pointer of the smaller element
                   i +=1 
               else: 
                   nums[k] = rightArray[j]
                   # incrementing the pointer of the larger element 
                   j +=1
               k +=1

           # for the left out elements we are performing it seperately 
           # Since in the above while loop if one condition stop satisfying loop breaks 
           # Then we need to merge next / remaining  elements   
           while i < len(leftArray): 
               nums[k] = leftArray[i] 
               i +=1
               k +=1
           # merging remaining elements of right half
           while j < len(rightArray): 
               nums[k] = rightArray[j] 
               j +=1
               k +=1

Java

class Solution {
    public int[] sortArray(int[] nums) {
        int n = nums.length;
        mergeSort(nums, 0, n - 1);
        return nums;
    }
    
    void mergeSort(int[] nums, int start, int end) {
        if (end - start + 1 <= 1) return; 
        int mi = start + (end - start) / 2;
        mergeSort(nums, start, mi);
        mergeSort(nums, mi + 1, end);
        merge(nums, start, mi, end);
    }
    
    void merge(int[] nums, int start, int mi, int end) {
        int lp = start;
        int rp = mi + 1;
        int[] buffer = new int[end - start + 1];
        // buffer pointer
        int t = 0; 
        while (lp <= mi && rp <= end) {
            // increment the left pointer 
            // if the right pointer element is bigger 
            // Since we are sorting in ascending order, left(smaller element) goes first
            if (nums[lp] < nums[rp]) {
                buffer[t++] = nums[lp++];
            } else {
                buffer[t++] = nums[rp++];
            }
        }
        // Since in the above while loop if one condition stop satisfying loop breaks 
        // Then we need to take care of  next / remaining  elements
        // merging remaining elements of left half 
        while (lp <= mi) buffer[t++] = nums[lp++];
        // Merging remaining elements of right half
        while (rp <= end) buffer[t++] = nums[rp++];
        // copy sorted buffer into original array
        for (int i = start; i <= end; i++) {
            nums[i] = buffer[i - start];
        }
    }
}

Bottom Up Approach / Iterative technique

Algorithm

• It starts with an element in the array. It is an iterative approach and because one item array is always sorted

• Compares two nearby elements to merge into a sorted subarray. Similarly, we then merge the sorted subarrays like we have done in top-down recursive approach (two-pointer approach)

• Continues until we have a sorted array

Java

class Solution {
    public List<Integer> sortArray(int[] nums) {
        List<Integer> res = new ArrayList<>();
        if (nums == null || nums.length == 0) return res;
        mergeSort(nums);
        for (int i : nums) res.add(i);
        return res;
    }    

    // iterative only 
    private void mergeSort(int[] nums) { 
        // here the size is doubled by 2
        // Since we are taking 2 elements at a time
        // That is the size of elements to be merged are becoming 2, 4, 8, 16 ...
        for (int size = 1; size < nums.length; size *= 2) {
            for (int i = 0; i < nums.length - size; i += 2 * size) {
                int mid = i + size - 1;
                int end = Math.min(i + 2 * size - 1, nums.length - 1);
                merge(nums, i, mid, end);
            }
        }
    }

    // Same as the merge function of the top down approach
    private void merge(int[] nums, int l, int mid, int r) {
        int[] tmp = new int[r - l + 1];
        int i = l, j = mid + 1, k = 0;
        while (i <= mid || j <= r) {
            if (i > mid || j <= r && nums[i] > nums[j]) {
                tmp[k++] = nums[j++];
            } else {
                tmp[k++] = nums[i++];
            }
        }
        // merging rest of the elements 
        // this code is same as that of top down approach of merging remaining elements
        System.arraycopy(tmp, 0, nums, l, r - l + 1);
    }
}

Merging of $n$ elements takes $n$ time and since each time the array is cut into half it takes $\log_{2}n$ time to reach the top. So total time complexity is $O(n\log_{2} n)$.

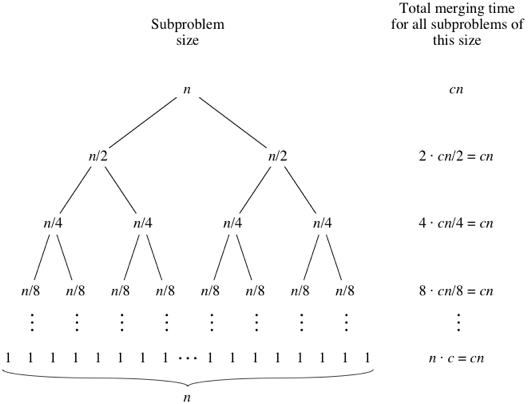
Image taken from Khan Academy

Merge Sort is a stable sort because the same element in an array maintain their original positions with respect to each other that means the original order of elements of input set is preserved.

Merge sort copies of more than a constant number of array elements. Hence it requires additional space which depends upon the input size of the array elements. So is an out of place algorithm.

Time Complexity: Best & Worst & Average is $O(n \log_{2} n)$

Space Complexity: $O(n)$

For very large arrays Merge sort is in effienct as it allocates an extra space of $O(n)$ so we should go for Quick sort.

Example: 0148 - Sort List

Given the head of a linked list, return the list after sorting it in ascending order.

Here we can follow both top-down and bottom-up merge sort.

Approach for Bottom-Up Merge Sort of Linked list

1. The two lists to be merged must be ordered respectively.
2. We can only start to merge two lists that only have one element.
3. Then we get an ordered list that has two elements
4. Do this again (that is "recursion").

Approach for Top-down Merge Sort of Linked list

1. Keep recursively dividing the list until there is only one node in the linked list.
2. Sort each sublist and merge each sorted sublist in a new array.
3. The two lists to be merged must be ordered respectively.
4. Here to order we must follow two pointer approach discussed above.

Steps to apply merge sort to a Linked list

Note: Implementation is based on Merge Sort on an array as discussed above.

1. Divide the linked list into two equal parts until when only one element is left.
2. To Divide, we need to find mid in the linked list using slow and fast pointers method.
3. Then merge the left and the right nodes of the linked list.

C++

/*
* Definition for singly-linked list.
* struct ListNode {
*     int val;
*     ListNode *next;
*     ListNode() : val(0), next(nullptr) {}
*     ListNode(int x) : val(x), next(nullptr) {}
*     ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
    void mergeSort(ListNode **head) {
        // create a current pointer
        ListNode *curr = *head ; 
        
        ListNode * left;
        ListNode * right;

        // if the linked list is null 
        // or the size is one return back the same
        if(curr == NULL || curr->next == NULL) return; 

        // call to find the middle node between left and right
        findMiddle(curr, &left, &right);
        
        // call merge_sort again to divide left half
        mergeSort(&left);
        
        // call merge_sort again to divide right half
        mergeSort(&right);
        
        // call to merge left and right by sorting them
        *head = merge(left, right);
    }

    void findMiddle(ListNode *curr, ListNode **left, ListNode **right) {
        // make a slow pointer
        ListNode* slow = curr;

        // make a fast pointer 
        ListNode* fast = curr-> next; 
        
        // then we move our fast up to it not become null
        while(fast != NULL) {
            fast = fast-> next;
            if(fast != NULL) {
                fast = fast-> next;
                slow = slow-> next;
            }
        }
        *left = curr;
        // right to slow next
        *right = slow-> next;

        // and slow next to null 
        slow-> next = NULL;         
    }

    ListNode* merge(ListNode* left, ListNode* right) {
        ListNode* res = NULL; 
        // Check if left is null, nothing to merge
        if(left == NULL) return right;

        if(right == NULL) return left;
    
        // if value of the left <= value of right
        // then res = left

        if(left-> val <= right-> val) {
            res = left;
            // and again call merge for res's next
            res-> next = merge(left-> next, right);     
        } else {
            res = right;
            // and again call merge for res's next
            res-> next = merge(left, right-> next);      
        }       
        return res;
    }

    ListNode* sortList(ListNode* head) {
        mergeSort(&head);
        return head;
    }
};

Suggested Problems

Problem Name	Difficulty	Solution Link
912-Sort an Array	Medium	View Solutions
56-Merge Intervals	Medium	N/A
148-Sort List	Medium	View Solutions
327-Count of Range Sum	Hard	View Solutions
23-Merge k Sorted Lists	Hard	View Solutions