2192 - All Ancestors of a Node in a Directed Acyclic Graph (Medium)
Problem Link
https://leetcode.com/problems/all-ancestors-of-a-node-in-a-directed-acyclic-graph/
Problem Statement
You are given a positive integer n representing the number of nodes of a Directed Acyclic Graph (DAG). The nodes are numbered from 0 to n - 1 (inclusive).
You are also given a 2D integer array edges, where edges[i] = [fromi, toi] denotes that there is a unidirectional edge from fromi to toi in the graph.
Return a list answer, where answer[i] is the list of ancestors of the ith node, sorted in ascending order.
A node u is an ancestor of another node v if u can reach v via a set of edges.
Example 1:
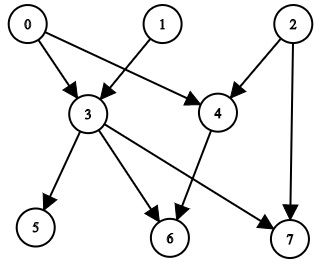
Input: n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
Output: [[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Nodes 0, 1, and 2 do not have any ancestors.
- Node 3 has two ancestors 0 and 1.
- Node 4 has two ancestors 0 and 2.
- Node 5 has three ancestors 0, 1, and 3.
- Node 6 has five ancestors 0, 1, 2, 3, and 4.
- Node 7 has four ancestors 0, 1, 2, and 3.
Example 2:
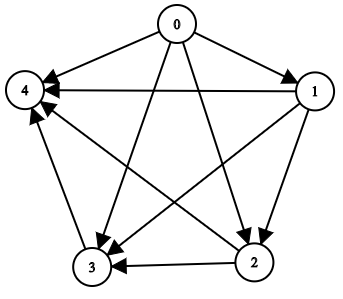
Input: n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Output: [[],[0],[0,1],[0,1,2],[0,1,2,3]]
Explanation:
The above diagram represents the input graph.
- Node 0 does not have any ancestor.
- Node 1 has one ancestor 0.
- Node 2 has two ancestors 0 and 1.
- Node 3 has three ancestors 0, 1, and 2.
- Node 4 has four ancestors 0, 1, 2, and 3.
Constraints:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- There are no duplicate edges.
- The graph is directed and acyclic.
Approach 1: Topological Sort
This question is quite challenging, and there are multiple ways to do it. Topological sort is one of the less direct way, but the logic is as following:
- Count the number of parents (In-Degree) of each node
- Start from the nodes without any parent
- For each child, remove one In-Degree of it, if it is zero, add it to the queue
- When looking at a node, perform union to the set of ancestors of each of its parent
We observe that we can be sure that the ancestors of a node are all found until all of its parents are visited. This is the reason why we only visit a node when its In-Degree (number of unvisited parent) is 0.
def getAncestors(self, n: int, edges: List[List[int]]) -> List[List[int]]:
#initialise the list of ancestors
ancestors = []
for i in range(n):
ancestors.append(set())
#initialize bfs level
level = set()
#initialize sets of parent, children, and in-degree
parents = defaultdict(list)
children = defaultdict(list)
degree = defaultdict(int)
for parent,child in edges:
parents[child].append(parent)
children[parent].append(child)
degree[child] += 1
#find the set of nodes without parents
for i in range(n):
if(i not in parents):
level.add(i)
#perform bfs
while(level):
newLevel = set()
for node in level:
#group all its parent's ancestors to node_ancestors
node_ancestors = set()
for parent in parents[node]:
node_ancestors |= ancestors[parent]
#need to include itself for its children to reference
node_ancestors.add(node)
#set the node's ancestors
ancestors[node] = node_ancestors
#update its child in-degree
for child in children[node]:
degree[child] -= 1
#if the child's parents have been visited, add it to next level
if(degree[child] == 0):
newLevel.add(child)
level = newLevel
ans = []
#put all ancestors to the final answer list
for i in range(n):
s = res[i]
#need to remove itself
s.remove(i)
l = list(s)
l.sort()
ans.append(l)
return ans
Approach 2: DFS
We can start from each node and perform DFS to find out all visited nodes. The ancestors of would be those visited nodes excluding . Since the searching direction is opposite, we change it from -> to -> . In Example 1, if is , then -> -> , -> -> and -> -> , so the visited nodes excluding itself are .
class Solution {
public:
vector<vector<int>> g;
vector<int> vis;
void dfs(int u) {
// mark it visited
vis[u] = 1;
// from u, check the next node
// e.g. node 6 can go to node 3 and node 4
for (auto v : g[u]) {
// only perform dfs if node is not visited
if (!vis[v]) {
dfs(v);
}
}
}
vector<vector<int>> getAncestors(int n, vector<vector<int>>& edges) {
g.resize(n);
vis.resize(n);
// from x[1] to x[0]
for (auto x : edges) g[x[1]].push_back(x[0]);
vector<vector<int>> ans;
for (int i = 0; i < n; i++) {
// tmp array to hold answer for node i
vector<int> tmp;
// vis is used to check if node i is visited or not
// re-init for each node
vis = vector<int>(n, 0);
// dfs - start from node i
dfs(i);
// right here all nodes from node i have been visited
// iterate each node
for (int j = 0; j < n; j++) {
// ancestors = those visited nodes excluding itself
if (!vis[j] || i == j) continue;
// node j is one of the ancestors
tmp.push_back(j);
}
// push it to ans
ans.push_back(tmp);
}
return ans;
}
};