2127 - Maximum Employees to Be Invited to a Meeting (Hard)

Problem Link

https://leetcode.com/problems/maximum-employees-to-be-invited-to-a-meeting/

Problem Statement

A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.

The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.

Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.

Example 1:

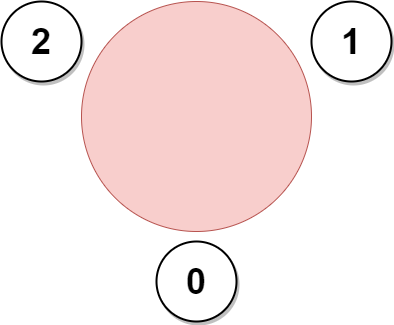
Input: favorite = [2,2,1,2]
Output: 3
Explanation:
The above figure shows how the company can invite employees 0, 1, and 2, and seat them at the round table.
All employees cannot be invited because employee 2 cannot sit beside employees 0, 1, and 3, simultaneously.
Note that the company can also invite employees 1, 2, and 3, and give them their desired seats.
The maximum number of employees that can be invited to the meeting is 3. 

Example 2:

Input: favorite = [1,2,0]
Output: 3
Explanation: 
Each employee is the favorite person of at least one other employee, and the only way the company can invite them is if they invite every employee.
The seating arrangement will be the same as that in the figure given in example 1:
- Employee 0 will sit between employees 2 and 1.
- Employee 1 will sit between employees 0 and 2.
- Employee 2 will sit between employees 1 and 0.
The maximum number of employees that can be invited to the meeting is 3.

Example 3:

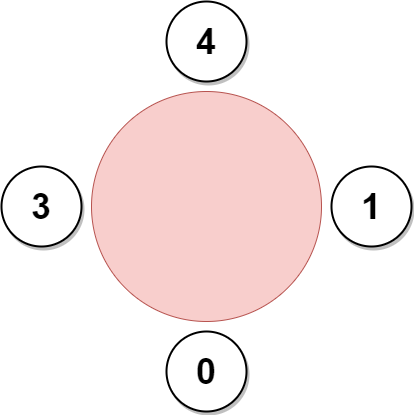
Input: favorite = [3,0,1,4,1]
Output: 4
Explanation:
The above figure shows how the company will invite employees 0, 1, 3, and 4, and seat them at the round table.
Employee 2 cannot be invited because the two spots next to their favorite employee 1 are taken.
So the company leaves them out of the meeting.
The maximum number of employees that can be invited to the meeting is 4.

Constraints:

• n == favorite.length
• 2 <= n <= 10^5
• 0 <= favorite[i] <= n - 1
• favorite[i] != i

Approach 1: DFS

If an employee A has a favourite person, let's say employee B, and vice versa. Then we can put them together. Then we can put an employee, let's say C, whose favourite person is A on the left hand side of A. Then put an employee, let's say D, whose favourite person is C next to C. If we do the same thing for employee B, then we can have two ways to extend. Therefore, we can first look for the interdependent nodes, in this case, A & B.

Starting from node A and node B, we perform dfs to calculate the maximum nodes of the left chain and the right chain. Then we could invite $left+right+2$people.

However, it would fail for the input [1,2,0] because it will output $0$ instead of $3$. In this case, we need to take care of the cyclic dependency. We need to run another dfs function for each node and check if there is a cyclic dependency. If the visited node is the entry node, then we know there is a cycle here. Then we could invite them also.

The final answer is simple the maximum number of the result of case 1 and case 2.

Written by @wingkwong

class Solution {
public:
    int maximumInvitations(vector<int>& a) {
        int n = a.size();
        vector<int> depth(n, -1);
        vector<vector<int>> inv(n);
        for (int i = 0 ; i < n; i++) inv[a[i]].push_back(i);
        // check interdependent nodes + longest left & right chain
        function<int(int)> dfs = [&](int u) {
            if (depth[u] != -1) return depth[u];
            int res = 0;
            for (int x : inv[u]) res = max(res, dfs(x));
            return depth[u] = res + 1;
        };
        int mx1 = 0, mx2 = 0;
        for (int i = 0; i < n; i++) {
            if (depth[i] != -1) continue;
            if (a[a[i]] == i) {
                depth[i] = depth[a[i]] = 0;
                int left = 0, right = 0;
                for (int x : inv[i])    if (x != a[i]) left  = max(left, dfs(x));
                for (int x : inv[a[i]]) if (x != a[i]) right = max(right, dfs(x));
                mx1 += left + right + 2;
            }
        }
        // check cyclic dependency
        function<tuple<int, int, int>(int)> dfs2 = [&](int u)->tuple<int, int, int> {
            if (depth[u] != -1) {
                return { u, depth[u], 0 };
            }  
            depth[u] = 0;
            auto [entry, d, isCyclic] = dfs2(a[u]);
            if (isCyclic) {
                return { entry, d, 1 };
            }
            depth[u] = d + 1;
            return {
                entry,
                depth[u],
                u == entry
            };
        };
        
        for (int i = 0; i < n; i++) {
            if (depth[i] != -1) continue;
            auto [entry, d, isCyclic] = dfs2(i);
            if (isCyclic) {
                mx2 = max(mx2, d);
            }
        }
        return max(mx1, mx2);
    }
};