2146 - K Highest Ranked Items Within a Price Range (Medium)
Problem Link
https://leetcode.com/problems/k-highest-ranked-items-within-a-price-range/
Problem Statement
You are given a 0-indexed 2D integer array grid of size m x n that represents a map of the items in a shop. The integers in the grid represent the following:
0represents a wall that you cannot pass through.1represents an empty cell that you can freely move to and from.- All other positive integers represent the price of an item in that cell. You may also freely move to and from these item cells.
It takes 1 step to travel between adjacent grid cells.
You are also given integer arrays pricing and start where pricing = [low, high] and start = [row, col] indicates that you start at the position (row, col) and are interested only in items with a price in the range of [low, high] (inclusive). You are further given an integer k.
You are interested in the positions of the k highest-ranked items whose prices are within the given price range. The rank is determined by the first of these criteria that is different:
- Distance, defined as the length of the shortest path from the
start(shorter distance has a higher rank). - Price (lower price has a higher rank, but it must be in the price range).
- The row number (smaller row number has a higher rank).
- The column number (smaller column number has a higher rank).
Return the k highest-ranked items within the price range sorted by their rank (highest to lowest). If there are fewer than k reachable items within the price range, return all of them.
Example 1:
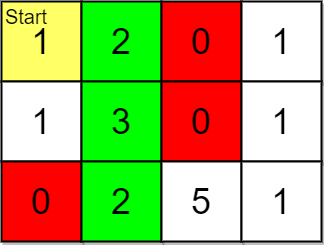
Input: grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
Output: [[0,1],[1,1],[2,1]]
Explanation: You start at (0,0).
With a price range of [2,5], we can take items from (0,1), (1,1), (2,1) and (2,2).
The ranks of these items are:
- (0,1) with distance 1
- (1,1) with distance 2
- (2,1) with distance 3
- (2,2) with distance 4
Thus, the 3 highest ranked items in the price range are (0,1), (1,1), and (2,1).
Example 2:
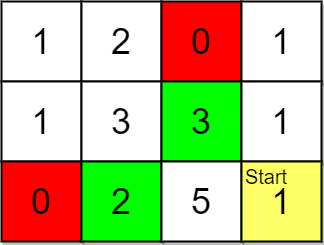
Input: grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
Output: [[2,1],[1,2]]
Explanation: You start at (2,3).
With a price range of [2,3], we can take items from (0,1), (1,1), (1,2) and (2,1).
The ranks of these items are:
- (2,1) with distance 2, price 2
- (1,2) with distance 2, price 3
- (1,1) with distance 3
- (0,1) with distance 4
Thus, the 2 highest ranked items in the price range are (2,1) and (1,2).
Example 3:
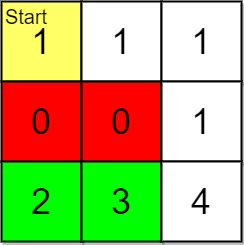
Input: grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
Output: [[2,1],[2,0]]
Explanation: You start at (0,0).
With a price range of [2,3], we can take items from (2,0) and (2,1).
The ranks of these items are:
- (2,1) with distance 5
- (2,0) with distance 6
Thus, the 2 highest ranked items in the price range are (2,1) and (2,0).
Note that k = 3 but there are only 2 reachable items within the price range.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10^51 <= m * n <= 10^50 <= grid[i][j] <= 10^5pricing.length == 22 <= low <= high <= 10^5start.length == 20 <= row <= m - 10 <= col <= n - 1grid[row][col] > 01 <= k <= m * n
Approach 1: BFS
This is a standard BFS problem. It is not difficult to implement but we need to pay attention on the requirements.
First we put our starting point to a queue. Then iterate the current queue and check if current cell grid[x][y] is within the price range. If so, we can put this cell to a temporary array for further processing. After that, we try to move in four directions. We need to check the new coordinate (next_x, next_y) is within boundary or not. Also we don't want to visit the same cell that we have already visited so we use vis[next_x][next_y] to check it. If it is not visited, we add the next cell to the queue and mark it as visited.
After we have the maximum k items, we need to sort them based on their rank from highest to lowest. We can apply a custom sorting comparator here. At the end, we output the coordinate of each cell. One thing to note that the reachable items can be less than k, hence we need to take the minimum one of tmp.size() and k.
class Solution {
public:
vector<vector<int>> highestRankedKItems(vector<vector<int>>& grid, vector<int>& pricing, vector<int>& start, int k) {
int n = grid.size(), m = grid[0].size();
vector<vector<int>> vis(n, vector<int>(m, 0));
vector<array<int, 3>> tmp;
queue<vector<int>> q;
q.push(start);
int dirx[4] = { -1, 0, 0, 1 };
int diry[4] = { 0, 1, -1, 0 };
vis[start[0]][start[1]] = 1;
int step = 0;
while (!q.empty() && tmp.size() < k) {
step++;
int sz = q.size();
for (int it = 0; it < sz; it++) {
vector<int> p = q.front(); q.pop();
int x = p[0], y = p[1];
if (0 <= x && x < n && 0 <= y && y < m && grid[x][y] != 0) {
if (pricing[0] <= grid[x][y] && grid[x][y] <= pricing[1]) {
tmp.push_back({x, y, step});
}
for (int d = 0; d < 4; d++) {
int next_x = x + dirx[d];
int next_y = y + diry[d];
if (0 <= next_x && next_x < n && 0 <= next_y && next_y < m && !vis[next_x][next_y]) {
vis[next_x][next_y] = 1;
q.push({next_x, next_y});
}
}
}
}
}
sort(tmp.begin(), tmp.end(), [&](const array<int, 3>& x, const array<int, 3>& y) {
return (x[2] < y[2]) ||
(x[2] == y[2] && grid[x[0]][x[1]] < grid[y[0]][y[1]]) ||
(x[2] == y[2] && grid[x[0]][x[1]] == grid[y[0]][y[1]] && x[0] < y[0]) ||
(x[2] == y[2] && grid[x[0]][x[1]] == grid[y[0]][y[1]] && x[0] == y[0] && x[1] < y[1]);
});
vector<vector<int>> ans;
for (int i = 0; i < min((int) tmp.size(), k); i++) {
ans.push_back({tmp[i][0], tmp[i][1]});
}
return ans;
}
};
In fact, a custom comparator is not necessary if we push the criteria in the same order to tmp, i.e. distance, price, row number and column number. This is because the sort() will sort them based on this order.
class Solution {
public:
vector<vector<int>> highestRankedKItems(vector<vector<int>>& grid, vector<int>& pricing, vector<int>& start, int k) {
int n = grid.size(), m = grid[0].size();
vector<vector<int>> vis(n, vector<int>(m, 0));
// vector<array<int, 3>> tmp;
vector<array<int, 4>> tmp;
queue<vector<int>> q;
q.push(start);
int dirx[4] = { -1, 0, 0, 1 };
int diry[4] = { 0, 1, -1, 0 };
vis[start[0]][start[1]] = 1;
int step = 0;
while (!q.empty() && tmp.size() < k) {
step++;
int sz = q.size();
for (int it = 0; it < sz; it++) {
vector<int> p = q.front(); q.pop();
int x = p[0], y = p[1];
if (0 <= x && x < n && 0 <= y && y < m && grid[x][y] != 0) {
if (pricing[0] <= grid[x][y] && grid[x][y] <= pricing[1]) {
// tmp.push_back({x, y, step});
tmp.push_back({step, grid[x][y], x, y});
}
for (int d = 0; d < 4; d++) {
int next_x = x + dirx[d];
int next_y = y + diry[d];
if (0 <= next_x && next_x < n && 0 <= next_y && next_y < m && !vis[next_x][next_y]) {
vis[next_x][next_y] = 1;
q.push({next_x, next_y});
}
}
}
}
}
sort(tmp.begin(), tmp.end());
// sort(tmp.begin(), tmp.end(), [&](const array<int, 3>& x, const array<int, 3>& y) {
// return (x[2] < y[2]) ||
// (x[2] == y[2] && grid[x[0]][x[1]] < grid[y[0]][y[1]]) ||
// (x[2] == y[2] && grid[x[0]][x[1]] == grid[y[0]][y[1]] && x[0] < y[0]) ||
// (x[2] == y[2] && grid[x[0]][x[1]] == grid[y[0]][y[1]] && x[0] == y[0] && x[1] < y[1]);
// });
vector<vector<int>> ans;
for (int i = 0; i < min((int) tmp.size(), k); i++) {
ans.push_back({tmp[i][2], tmp[i][3]});
}
return ans;
}
};
Time Complexity: O(m * n * logk)
Space Complexity: O(m * n)