0097 - Interleaving String (Medium)

Problem Link

https://leetcode.com/problems/interleaving-string/

Problem Statement

Given strings s1, s2, and s3, find whether s3 is formed by an interleaving of s1 and s2.

An interleaving of two strings s and t is a configuration where s and t are divided into n and m substrings respectively, such that:

• s = s1 + s2 + ... + sn
• t = t1 + t2 + ... + tm
• |n - m| <= 1
• The interleaving is s1 + t1 + s2 + t2 + s3 + t3 + ... or t1 + s1 + t2 + s2 + t3 + s3 + ...

Note: a + b is the concatenation of strings a and b.

Example 1:

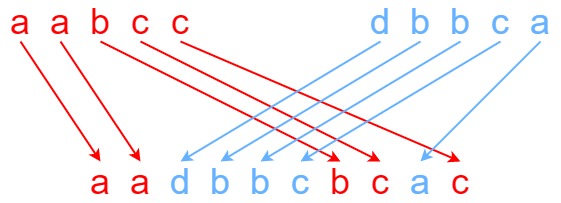
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Explanation: One way to obtain s3 is:
Split s1 into s1 = "aa" + "bc" + "c", and s2 into s2 = "dbbc" + "a".
Interleaving the two splits, we get "aa" + "dbbc" + "bc" + "a" + "c" = "aadbbcbcac".
Since s3 can be obtained by interleaving s1 and s2, we return true.

Example 2:

Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false
Explanation: Notice how it is impossible to interleave s2 with any other string to obtain s3.

Example 3:

Input: s1 = "", s2 = "", s3 = ""
Output: true

Constraints:

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1, s2, and s3 consist of lowercase English letters.

Follow up: Could you solve it using only O(s2.length) additional memory space?

Approach 1: 2D Dynamic Programming

If we try to break down our problem into a sub problem we get that we are trying to find whether the characters in $s1$ up to $i$ and the characters in $s2$ up to $j$ can interleave to create a string in $s3$ up to $i + j$.

So to construct our 2D grid we would need a grid of size $s2.length + 1$ wide and $s1.length + 1$ tall of all false/falsy values. This allows us to account for the empty string prefix of both $s1$ and $s2$. We would then initialize the $0,0$ position as a true/truthy value, as we know we can create the empty $s3$ using the empty $s1$ and $s2$ strings.

For $i,j$ values in our grid, it maps out $i$ values to position is $s1$ and $j$ values to position in $s2$. This means that for each $i,j$ value in our grid it tells us whether we can create $s3[:i+j]$ using the characters from $s1[:i]$ and $s2[:j]$.

So then for each i,j we know if it isn't the first row or column (our empty string values), and that if the character from the previous iteration of $s1$ matches the previous iteration character of $s3$

Time Complexity: $O(n*m)$ where $n$ is the length of $s1$ and $m$ is the length of $s2$. We are iterating over our dp array of size $n*m$.

Space Complexity: $O(n*m)$. Our dp array will be of size $n*m$.

Python

Written by @ColeB2

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        # return early if s1 and s2 combined aren't same size as s3.
        if len(s1) + len(s2) != len(s3):
            return False
        
        # create our 2d grid, we need an extra row/col to account for
        # the empty string case when comparing either empty s1/s2 values.
        dp = [[0 for _ in range(len(s2) + 1)] for _ in range(len(s1) + 1)]
        # initialize first value to be truthy, as we know we can create
        # s3="" using s1="" and s2="". This is the initial base case of
        # interleaving 2 empty string to equal an empty string.
        dp[0][0] = 1
        # loop through the 2d dp array. Remembering the first row/col
        # handles the empty string sub-problems.
        for i in range(len(s1) + 1):
            for j in range(len(s2) + 1):
                # check 3 things for each position in s1, s2.
                #1. i/j > 0: We can't check positions of less than
                # the empty "" string value. i/j == 0, that handles
                # empty strings, and their is no way to be < empty.
                #2. Check string value at s1[i-1] == s3[i+j-1]. This
                # is checking if the letters at the proper position are
                # equal. Note we subtract 1, since we added a extra 
                # row/col to the start of each row/col in dp table.
                #3. And if prevs 2 are truthy, We check that it held the
                # same for the previous i value.
                if i > 0 and s1[i-1] == s3[i+j-1] and dp[i-1][j]:
                    # if so, we can call this true/truthy
                    dp[i][j] = 1
                if j > 0 and s2[j-1] == s3[i+j-1] and dp[i][j-1]:
                    dp[i][j] = 1
        # the full string would be represented by the length os s1,s2
        # in our dp table.
        return dp[len(s1)][len(s2)]