0073 - Set Matrix Zeroes (Medium)

Problem Link

https://leetcode.com/problems/set-matrix-zeroes/

Problem Statement

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0's.

You must do it in place.

Example 1:

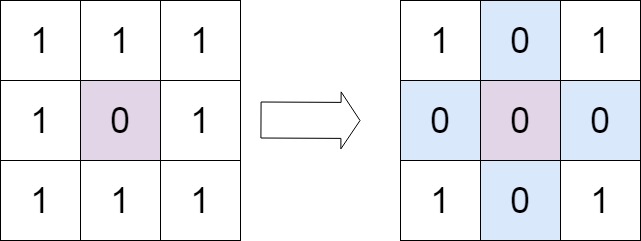
Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:

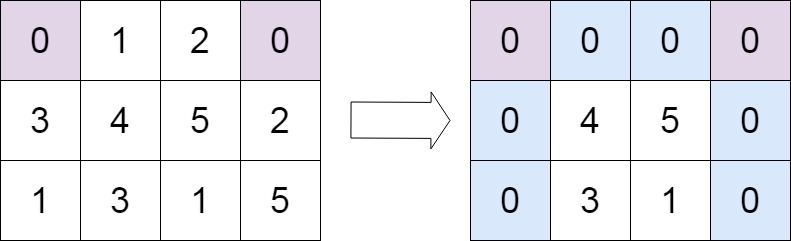
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

Constraints:

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -2^31 <= matrix[i][j] <= 2^31 - 1

Follow up:

• A straightforward solution using O(mn) space is probably a bad idea.
• A simple improvement uses O(m + n) space, but still not the best solution.
• Could you devise a constant space solution?

Approach 1: Inplace, Constant Space, Iteration.

To save space, we can just iterate over the entire matrix initially, if we ever reach a $0$, we can record that in the top row/left column, by rewriting it with a $0$. Then we can check the top row, left column at the end, and rewrite all rows/columns that have a top row/left column as $0$.

The edge case you can imagine is how we handle the top left corner. If we have a $0$ in the first row/first column and place a $0$ in the first row/column, then when we replace all numbers afterwards, we are going to ruin our tracking method.

To handle this, we can use a boolean to track if the first row/first column has zeroes, iterate the first/row column, and update the boolean of the first row/column has a $0$. From then on, we can do as we described above, just starting at $1$ for both the row/column, as we already handled the first row/column.

Finally, we can rewrite everything, again starting at $1$ for both the row/column, and handling the first row/column at the end, based on the boolean values we found earlier.

Time Complexity: $O(m * n)$. Where $m$ is the number of rows, and $n$ is the number of columns. We must iterate over the whole matrix a couple of times.

Space Complexity: $O(1)$. We can do it in constant extra space, by using the first row/column to track which rows and columns are zeroed out and using boolean values to handle the first row/column.

Python

Written by @ColeB2

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        # Track our rows and columns.
        ROWS, COLS = len(matrix), len(matrix[0])
        # iterate first column, if any value is 0, set first_col to True.
        # python any method will set first_row to a boolean, based on
        # if the condition we provided ever occurs, we can then also
        # loop through all the values and check.
        first_row = any(matrix[0][c] == 0 for c in range(COLS))
        # iterate first row to check for 0's, if any value is a 0, then
        # the first column needs to be zeroed out.
        first_col = any(matrix[r][0] == 0 for r in range(ROWS))
        # Note above: Our first row, will be all the values in
        # the row going horizontally, which means we are checking
        # the value of each column in row 0, similarly, our first
        # column will be all the values in the column going vertically,
        # so we check the value of each row in column 0.
        
        # Iterate our matrix, skipping the first row/column
        for r in range(1, ROWS):
            for c in range(1, COLS):
                # found a 0, set the first/row column value to 0
                if matrix[r][c] == 0:
                    matrix[r][0] = 0
                    matrix[0][c] = 0
        # Set the row/columns to zeroes. Again iterate matrix, skipping
        # the first row/column
        for r in range(1, ROWS):
            for c in range(1, COLS):
                # if either the first row of any given cell or
                # the first column of any given cell is 0, we can 
                # set the current cell to 0.
                if matrix[r][0] == 0 or matrix[0][c] == 0:
                    matrix[r][c] = 0
        # Edge cases, if the first row was 0, set all column values in 
        # the top row to 0.
        if first_row:
            for c in range(COLS):
                matrix[0][c] = 0
        # if first_column contained a 0, set all row values in the left
        # column to 0.
        if first_col:
            for r in range(ROWS):
                matrix[r][0] = 0