0079 - Word Search (Medium)

Problem Link

https://leetcode.com/problems/word-search/

Problem Statement

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

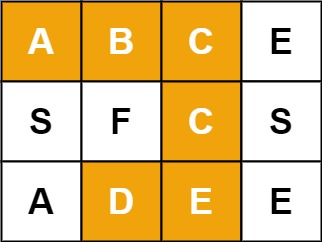
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

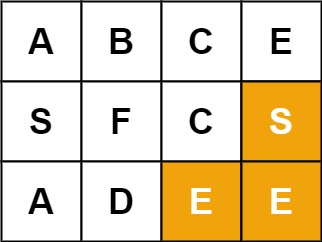
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board and word consists of only lowercase and uppercase English letters.

Follow up: Could you use search pruning to make your solution faster with a larger board?

Approach 1: Backtracking

To solve this, we can very simply traverse the board, and when we find our starting letter, run our backtracking/DFS function at that letter, and if we find the word, return True.

Inside our DFS, we would need to track some edge cases, if our position on the board is within bounds, if we have visited that position on the board before, and that the character we are looking at is the letter we need, and if everything checks out, we can check all 4 adjacent corners.

Depending on how it is implemented though, the backtracking solution will be very slow, or even TLE. That is where the follow-up of search pruning comes into play.

There are 3 things we can edge cases we can check to ensure our algorithm is efficient.

1. First, we can check if the word is larger than the number of characters on the board. If so we have no reason to continue.
2. Second, we can count both the characters on the board and in the word and compare the 2. If a character in the word isn't on the board, or there isn't enough of them on the board, we can terminate early again.
3. Finally, we can flip the word if there are fewer characters on the board of the word's last letter, than its first we can flip the word. For example: If we have the word $cat$ and our board has a lot of $c$ characters, and only 1 $t$ character, it makes more sense to search for the $t$ character, as we will only have to run our DFS algorithm once, instead of several times for each $c$ we find.

Time Complexity: $O(m*n*3^L)$ Where m is the number of rows, n is the number of columns, and L is the length of the word. Note it is $3^L$ instead of 4, as after the first DFS call, we only check 3 paths, as the 4th path would be a visited position that will terminate early.

Space Complexity: $O(L)$ for our DFS call stack and our visited set, where L is the length of the word as the size of those will depend on the length of our word. The pruning also adds $O(L + m*n)$ to create Counters for the word, and the board.

Python

Written by @ColeB2

class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        ROWS, COLS = len(board), len(board[0])
        # 1st search pruning: word is larger than the board.
        if len(word) > ROWS*COLS:
            return False
        # get counter of all characters on the board
        board_chars = {}
        for r in range(ROWS):
            for c in range(COLS):
                if board[r][c] not in board_chars:
                    board_chars[board[r][c]] = 0
                board_chars[board[r][c]] += 1
        # counter of all characters in word
        word_chars = Counter(word)
        # 2nd search pruning: For each letter in our word, there
        # isn't enough on the board to create the word.
        for ch in word_chars:
            if ch not in board_chars or board_chars[ch] < word_chars[ch]:
                return False
        # 3rd search pruning: If there are less characters on the
        # board of the character than the first, flip the word.
        if (word[0] in board_chars and word[-1] in board_chars
            and board_chars[word[0]] > board_chars[word[-1]]
            ):
            word = word[::-1]
        # DFS function
        def dfs(row, col, idx, visited):
            # Reached end of word, found the word statement
            if idx == len(word):
                return True
            # False clauses, boundary check, already visited, wrong letter.
            if (row < 0 or col < 0
                or row == ROWS or col == COLS
                or (row,col) in visited
                or board[row][col] != word[idx]
                ):
                return False
            # add the position to the visited set
            visited.add((row,col))
            # check all 4 positions
            if (dfs(row + 1, col, idx + 1, visited) or
                dfs(row - 1, col, idx + 1, visited) or
                dfs(row, col + 1, idx + 1, visited) or
                dfs(row, col - 1, idx + 1, visited)
                ):
                # if 1 is true, we found the word.
                return True
            # backtrack, remove the current position from set.
            visited.remove((row,col))
        # search the board looking for first character to start DFS.
        for r in range(ROWS):
            for c in range(COLS):
                if board[r][c] == word[0]:
                    if dfs(r,c, 0, set()):
                        return True
        # Reach the end, didn't find the word, return False.
        return False