0110 - Balanced Binary Tree (Easy)

Problem Link

https://leetcode.com/problems/balanced-binary-tree/

Problem Statement

Given a binary tree, determine if it is height-balanced.

For this problem, a height-balanced binary tree is defined as:

a binary tree in which the left and right subtrees of every node differ in height by no more than 1.

Example 1:

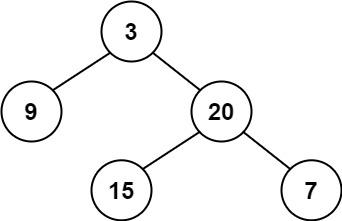
Input: root = [3,9,20,null,null,15,7]
Output: true

Example 2:

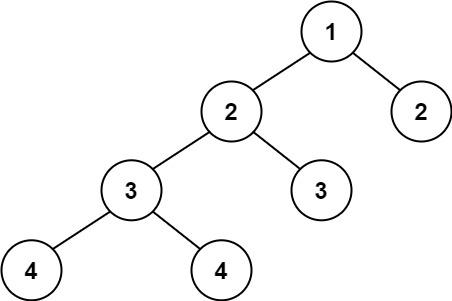
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false

Example 3:

Input: root = []
Output: true 

Constraints:

• The number of nodes in the tree is in the range [0, 5000].
• -10^4 <= Node.val <= 10^4

Visualization

Approach 1: Straight forward - Recursion

This solution is strictly following the definition of a balanced binary tree.

• (1) ABS(left sub-tree's height - right sub-tree's height) $<= 1$.

• (2) Every left sub-trees and right sub-trees are also balanced.

First, we need to set up the base case for the recursion solution. Then we check if the whole left subtree and right subtree are balanced. If so, then we check if every subtrees are balanced.

Time Complexity: $O(n)$ as recursively we are going to have to process each node inside the tree at least once using a depth-first approach.

Space Complexity: $O(h)$ as using a recursive DFS solution will only ever hold the current path inside our call stack, which will scale with the height of the tree.

Java

Written by @SkollRyu

class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        if(Math.abs(height(root.left) - height(root.right)) <= 1){
            return isBalanced(root.left) && isBalanced(root.right);
        } else {
            return false;
        }
    }
    
    public int height(TreeNode root){
        if (root == null) return -1;
        int ld = height(root.left);
        int rd = height(root.right);
        return 1 + Math.max(ld,rd);
    }
}

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # We will use Truthy values for our return here. Meaning if we return any 
    # number that isn't 0, the judge will consider is similar as returning True.
    # And if we return 0/False, the judge will consider it as a False value.
    def isBalanced(self, root: Optional[TreeNode]) -> bool:
        # Base case null node: 
        # We will use 1 as height of null node here as it accomplishes 2 things: 
        # 1. it passes up a height value for child nodes,
        #    Ex. For a child node. If we calculate the left/right height 
        #    difference, it will come out to 0 regardless if we use 0-0 or 1-1.
        # 2. it acts as a 'Truthy' value for the 'null tree'
        #    Ex. if our initial input is null, ie an empty tree. It is considered
        #    balanced, and the 1 value acts as a 'Truthy' value to return True.
        if not root:
            return 1
        # Find the height of the left sub-tree - recursively.
        left = self.isBalanced(root.left)
        # if left sub-tree is ever False, stop. No need to continue.
        if not left:
            return False
        # Find the height of the right sub-tree - recursively.
        right = self.isBalanced(root.right)
        # if right sub-tree is ever False, stop. No need to continue
        if not right:
            return False
        # Calculate the height differences. If they are ever > 1: not balanced.
        if abs(left - right) > 1:
            return False
        # Return height of longest subtree up for further calculations.
        return max(left, right) + 1