0100 - Same Tree (Easy)

Problem Link

https://leetcode.com/problems/same-tree/

Problem Statement

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:

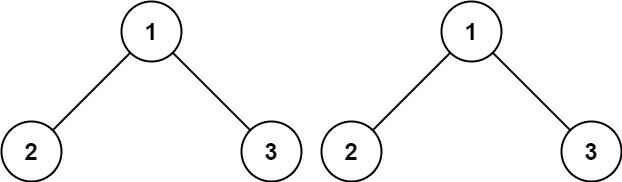
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:

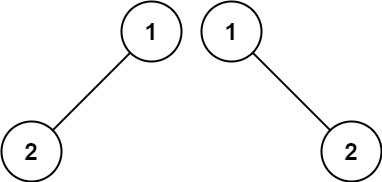
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:

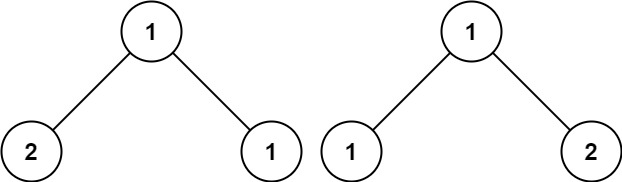
Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

• The number of nodes in both trees is in the range [0, 100].
• -10^4 <= Node.val <= 10^4

Approach 1: Recursive Depth-First Search

Very simply, a tree, $p$ is the same as a tree, $q$ if the structure of both trees is identical, and the values of the nodes are the same. Meaning at each step we must make sure:

1. p and q are both currently nodes, and their values are equal. If so, we can continue to check their subtrees.
2. If 1 isn't true. Then check if they are null nodes. If so we can return True. If one is null and the other isn't then we must return False.

We can do the above as a recursive DFS solution.

Time Complexity: $O(n)$ where n is the number of nodes in p/q. Since in the worst case, they will be completely similar trees, except for 1 child node, we will have to traverse each node in each tree.

Space Complexity: $O(h)$ where h is the height of the tree. As by using a recursive DFS solution, we will only ever hold the current path inside our recursive call start, which will scale with the height of the tree.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        # Check that p exists, q exists, and if they both exist that the values
        # of the nodes are equal.
        if p and q and p.val == q.val:
            # If they are equal, recursively check left sub-tree of each node
            # together and the right sub-tree of each node together.
            return self.isSameTree(p.left, q.left) and self.isSameTree(p.right,q.right)
        # If above is false, we must check to see if they are either both null
        # nodes, or if 1 is a child node and the other isn't
        # In Python p is q will handle both cases.
        # if both are None --> return True
        # if 1 is a node and the other is None, it will return False.
        return p is q

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function(p, q) {
    // if both of them are empty
    if (!p && !q) return true;
    // if one of them is empty 
    // if the values are not the same
    if (!p || !q || p.val != q.val) return false;
    // recursive call
    // are left and right subtree equal
    return (isSameTree(p.left, q.left) && 
            isSameTree(p.right, q.right));
};

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        // if both of them are empty
        if (!p && !q) {
            return true;
        }
        // if one of them is empty 
        // if the values are not the same
        if (!p || !q || p->val != q->val) {
            return false;
        }
        // recursive call
        // are left and right subtree equal
        return (isSameTree(p->left, q->left) &&
                isSameTree(p->right, q->right));
    }
};

Approach 2: Iterative Depth-First Search

Similar to the recursive approach above, we just have to create and maintain our own stack instead of utilizing the call stack.

Time Complexity: $O(n)$ similar to above, we must traverse each node of p/q to check they are the same.

Space Complexity: $O(h)$ also similarly, although with our own stack, we will only ever have the current path we are traversing in the stack.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        # initialize our own stack to maintain, start with tuple of (p,q)
        stack = [(p,q)]
        # while the stack contains values:
        while stack:
            # pop of the nodes and assign them to two variables, we will use n,m.
            n,m = stack.pop()
            # if n and m are both nodes and the values are equal:
            if n and m and n.val == m.val:
                # add left sub-tree of n and m to the stack
                stack.append((n.left, m.left))
                # add right sub-tree of n and m to the stack
                stack.append((n.right, m.right))
            # if n does not equal m. Meaning either:
            # n/m is a null node and the other isn't
            # or both n and m have different values.
            elif n != m:
                # terminate early, return False
                return False
        # made it through the loop with no termination, which means the trees are
        # the same. return True.
        return True

C++

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        stack<pair<TreeNode*, TreeNode*>> st;
        st.push({p, q});
        while (!st.empty()) {
            auto [node1, node2] = st.top();
            st.pop();
            if (!node1 && !node2) continue;
            if (!node1 || !node2 || node1->val != node2->val) {
                return false;
            } else {
                st.push({node1->left, node2->left});
                st.push({node1->right, node2->right});
            }
        }
        return true;
    }
};