Skip to main content

0104 - Maximum Depth of Binary Tree (Easy)

https://leetcode.com/problems/maximum-depth-of-binary-tree

Problem Statement​

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

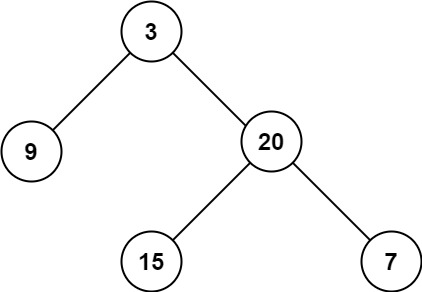
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [0, 104].
  • -100 <= Node.val <= 100

Approach 1: Recursive​

Traverse left and right nodes till last, and at every level keep find the maximum between left and right nodes and add 1.

Written by @vigneshshiv
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
// Time complexity: O(n), where n - # of nodes in the tree
// Space complexity: O(h), where h - height of the tree from root
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) return 0;
        return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
    }
}

We can solve this iteratively by tracking a global max and using a stack to store our data for each node. What we will store is the node we are processing itself and the depth of that node. Then while traversing, we can update the global max depth on each iteration, and return it at the end.

While traversing the tree we can process each node by:

  1. Updating the global max depth by checking whether the depth of the current node is larger or not, we can do this using the max function.
  2. Checking whether it has children nodes, then adding them to the list, making sure the depth of the child node is 1 greater than the current node.

Time Complexity: O(n)O(n) where n is the number of nodes. We have to process each node once.

Space Complexity: O(h)O(h) where h is the height of the tree. Since we are only storing the nodes of the current path we are traversing.

Written by @ColeB2
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # Early termination, if given none as a root, return early.
        if not root:
            return 0
        # initialize stack with root and starting depth of 1.
        stack = [(root,1)]
        # track our global max_depth
        max_depth = 1
        # traverse our tree while our stack has values.
        while stack:
            # pop off the node and the count of the current depth.
            node, count = stack.pop()
            # update the max depth.
            max_depth = max(count, max_depth)
            # if the node has a left child
            if node.left:
                # add it to the stack, update the depth of the child node.
                stack.append((node.left, count+1))
            # if node has right child
            if node.right:
                # add it to the stack, update depth of the child node.
                stack.append((node.right, count+1))
        # return the max depth we found.
        return max_depth

We can also use a queue as our main data structure. A queue allows us to traverse the tree 1 level at a time. Meaning instead of updateing the global max depth at each node, we can update it once at each level.

While traversing the tree we can process each level by:

  1. Updating the max depth we have reached.
  2. Running a for loop over the length of the queue. This allows us to process each node currently in the queue, while also adding the children node to the queue.
  3. During the processing of each node, make sure it has children before adding them to the queue.

Time Complexity: O(n)O(n) where n is the number of nodes. We have to process each node once.

Space Complexity: O(n)O(n) where n is the number of nodes, as in a full tree, the last layer will hold n2\frac {n}{2} nodes.

Written by @ColeB2
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # Early termination, given a null root.
        if not root:
            return 0
        # initialize our queue with the root node.
        q = deque([root])
        # track a global max depth.
        max_depth = 0
        # traverse the tree while nodes exist in the queue.
        while q:
            # update the max depth
            max_depth += 1
            # traverse each node in the queue. Ex. If the current level has
            # 4 nodes inside the queue, then we will only loop 4 times, despite
            # also adding extra nodes to the queue during each loop.
            for _ in range(len(q)):
                # pop the node we want to process
                node = q.popleft()
                # left child check before adding it to the queue.
                if node.left:
                    q.append((node.left))
                # right child check.
                if node.right:
                    q.append((node.right))
        # return our maximum depth
        return max_depth