0102 - Binary Tree Level Order Traversal (Medium)

Problem Link

https://leetcode.com/problems/binary-tree-level-order-traversal/

Problem Statement

Given the $root$ of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

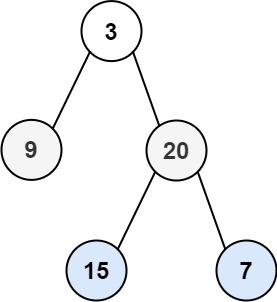
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 2000].
• -1000 <= Node.val <= 1000

Approach 1: BFS

• Take one 2D vector $ans$ to return the final tree-traversal, and another vector $v$ to store seperate levels.
• Take a queue, store $root$ node inside it and a NULL node for seperating levels.
• Until the queue is not empty, pop one by one nodes from queue. if the node is NULL and queue is not empty, push the NULL again inside the queue. Push $v$ into $ans$ as one level is completed and clear $v$.
• If the node is not null, push the value into $v$ and push its left and right nodes into queue (if not null).

Time Complexity: $O(N)$
All the nodes of the binary tree (N nodes) are traversed once at a time. So, $O(N)$ time complexity is needed to traverse all the $N$ nodes.

Space Complexity: $O(N)$
A queue data structure is taken to store the next level nodes. For the worst case, the queue is stored with all the $N$ nodes. That's why the space complexity is $O(N)$.

C++

Written by @Srijita-Mandal

class Solution {
    public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ans;
        // return [] if the input is null
        if (root == NULL) return ans;
        
        //for storing each level
        vector<int> v;  
        queue<TreeNode*> q;
        // starting point
        q.push(root);
        // for sepearting levels
        q.push(NULL);  

        // BFS
        while(!q.empty()){
            TreeNode* cur = q.front();
            q.pop();
            if (cur == NULL) {
                // storing each level into ans vector
                ans.push_back(v);  
                // clearing v vector to insert next level
                v.clear();  
                // storing NULL at the end of queue
                if (!q.empty()) q.push(NULL); 
            } else{
                v.push_back(cur->val);
                if (cur->left != NULL) q.push(cur->left);
                if (cur->right != NULL) q.push(cur->right);
            }
        }
        return ans;
    }
};

Python

Written by @radojicic23

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        res = []
        # initialize queue
        q = collections.deque()
        # add root node that we are given in queue
        q.append(root)
        
        # BFS
        while q:
            level = []
            # going through one level at a time 
            # with those nodes from that level
            # we are going to add them to it's own list (level)
            # and we are going to add that list to the result 
            for i in range(len(q)):
                # pop nodes from the left of the queue
                node = q.popleft()
                # if node is not empty 
                if node:
                    level.append(node.val)
                    # add children of this node to queue
                    q.append(node.left)
                    q.append(node.right)
            # if level is not empty
            if level:
                # add level to the result 
                res.append(level)
        return res 

JavaScript

Written by @radojicic23

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
var levelOrder = function(root) {
    let q = [root];
    let res = [];
    // BFS
    while (q[0]) {
        let level = [];
        let q_len = q.length;
        // going through one level at a time 
        // with those nodes from that level
        // we are going to add them to it's own list (level)
        // and we are going to add that list to the result
        for (let i = 0; i < q_len; i++) {
            // pop nodes from the left of the queue
            let node = q.shift();
            level.push(node.val);
            // add children of this node to queue
            if (node.left) q.push(node.left);
            if (node.right) q.push(node.right);
        }
        // add level to the result 
        res.push(level);
    }
    return res;
};