0124 - Binary Tree Maximum Path Sum (Hard)

Problem Link

https://leetcode.com/problems/binary-tree-maximum-path-sum/

Problem Statement

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

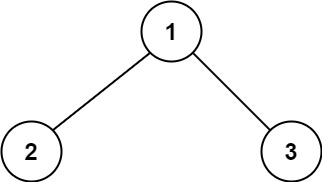
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

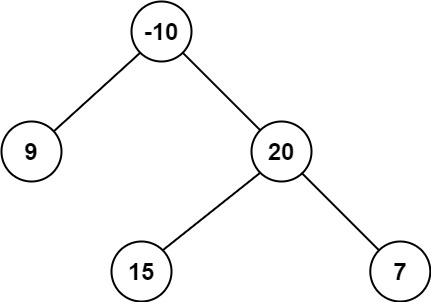
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 10^4].
• -1000 <= Node.val <= 1000

Approach 1: Depth-First Search

The easiest approach is going to be able to pass up values from the bottom up. That makes this a good reason to use a recursive depth-first search. We can reach the bottom of the tree, then pass up the max path from the left and right nodes.

The only other little trick is knowing that the max path sum can only contain 2 edges means the path may not reach straight up to the root. So we must also update a global max with our local max. This would be the current node, plus both subtrees values. We won't pass this one up, but it may still possibly be the max path.

Time Complexity: $O(n)$, we must process each node in the binary tree.

Space Complexity: $O(h)$, we are using a recursive DFS, so it will scale with the high of the tree to track our recursive call stack. This means in the worst case $h$ will be equal to $n$.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:

    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        # initialize a variable to track max path. We will start with our root
        # value, as that is a possible path.
        max_path_sum = root.val
        def helper(node: Optional[TreeNode]) -> int:
            #base case - reach null node, return 0.
            if not node:
                return 0
            # nonlocal brings our max_path_sum variable into function
            nonlocal max_path_sum
            # recursively get max path of our left and right subtrees
            left = helper(node.left)
            right = helper(node.right)
            # select the larger path of the left/right trees.
            local_max_path = max(left, right)
            # return path value --> update it with our node value
            # if and only if our local max is positive. Otherwise
            # we will just use our node value as local max.
            path = local_max_path + node.val if local_max_path > 0 else node.val
            # Update our global max, we will use 3 parameters. Local max that we are
            # going to pass up, the global max, and lastly, the path from the
            # current node that goes both left and right.
            max_path_sum = max(path, max_path_sum, (left+right+node.val))
            # we can't pass up the value that goes both left and right,
            # so we pass up our path variable which is the current node
            # and/or the max path of the left/right trees, if non-negative.
            return path
        # call our helper function and return our answer.
        helper(root)
        return max_path_sum