0105 - Construct Binary Tree from Preorder and Inorder Traversal (Medium)

Problem Link

https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

Problem Statement

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

Example 1:

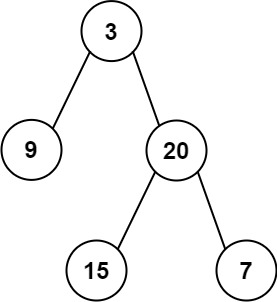
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

Constraints:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder and inorder consist of unique values.
• Each value of inorder also appears in preorder.
• preorder is guaranteed to be the preorder traversal of the tree.
• inorder is guaranteed to be the inorder traversal of the tree.

Approach 1: Recursion and Array Slicing

This problem can be solved with simple recursion if we make some observations. The first is noticing that the first value in preorder is always our root node. The second is noticing that our root order splits the inorder array into left and right halves. Knowing that we can repeatedly slice our array and pass the slices back into our recursive algorithm.

The big question is how we slice. Noticing the first in preorder is always the node means the left side will always need to slice the first piece off. If we call the middle split of the 2 halves by a variable $m$, then we know that if preorder must also remove the front number, then we must split it around $m+1$ where as inorder needs to be sliced around our root value, being $m$ and $m+1$

Index:      0    1  2  3  4  5  6  7
preorder = (7) -10 -4  3 -1  2 -8 11
inorder  = -4   10  3 -1  7 11 -8  2

If 7 is our root, we can see, to maintain even partitions, we need to split the first array from 1-5(non-inclusive), and the second array from 0-4(non-inclusive).

Index:      0|  1  2  3  4|     5  6  7
preorder =  7|-10 -4  3 -1|     2 -8 11
            0   1  2  3  4|
inorder  = -4  10  3 -1 |7|    11 -8  2
                         m=4

Note above: preorder must splice off the first number, and must contain the index of our root in inorder. Whereas inorder the left half splices up to the root, then skips the root and splices from $m+1$ to the end.

Time Complexity: $O(n)$. The time will scale with n, the number of nodes in our tree. Note that array slicing takes up time as well, so it can be made much more efficient by tracking endpoints around the slices instead.

Space Complexity: $O(n)$. The array slices at each iteration will take up space, as well as our call stack, which will scale with height, but approach $n$ in worst case scenarios.

Python

Written by @ColeB2

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        # Base case, if preorder None it means we have no nodes to create
        # if inorder is none, it means we have no children on either side.
        # both cases we can return None.
        if not preorder or not inorder:
            return None
        # The Value of the node we need to create
        val = preorder[0]
        # Create the tree node
        root = TreeNode(val)
        # Find the index of the value in inorder.
        m = inorder.index(val)
        # Recursively create the left and right trees.
        # Preorder: Must remove the first value, then to match it with the inorder
        # we must splice it up to m+1
        # Inorder: Splice it up to m, then we must skip the root as it has been
        # use already. So we splice the right half from m+1 to avoid double
        # counting the root.
        root.left = self.buildTree(preorder[1 : m + 1], inorder[:m])
        root.right = self.buildTree(preorder[m + 1:], inorder[m + 1:])
        # return our root.
        return root