0133 - Clone Graph (Medium)

Problem Link

https://leetcode.com/problems/clone-graph/

Problem Statement

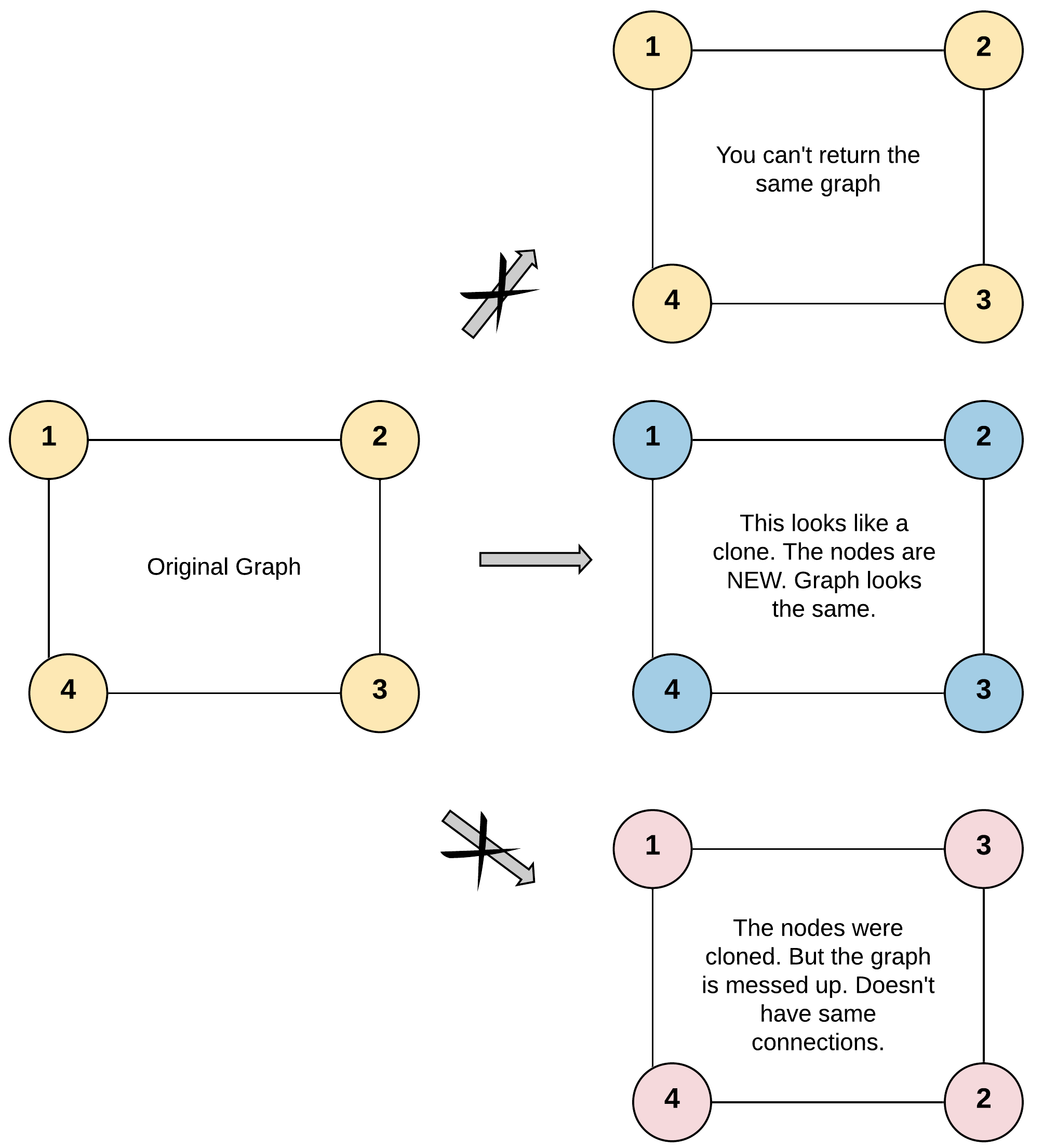
Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.

An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

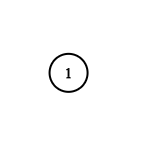
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Constraints:

• The number of nodes in the graph is in the range [0, 100].
• 1 <= Node.val <= 100
• Node.val is unique for each node.
• There are no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

Approach 1: Iterative Depth/Breadth-First Search

We need to traverse all the nodes in the graph, create copies, and connect the copies. Iteratively we can use a stack or a queue to traverse nodes we haven't visited already.

Starting at the first node, we will traverse by checking all the neighbors of the nodes. For each neighbor, we will get/create ae copy of that neighbor and add the copied neighbour to the neighbour of the node we are looking at.

We will also want to check if the neighbour has been added to our hash map. If not, we can add it to our queue/stack to visit it and its neighbors, as well as add it to the hash map with its copy.

Time Complexity: $O(V + E)$. Where $V$ is the number of nodes, and $E$ is the number of edges in the graph. We will visit each vertex/node once during our BFS/DFS, and while looking through the neighbors, we will check on each edge twice. Once for each neighbor.

Space: $O(V)$ Our hash map, and stack/queue will take $O(V)$ space.

Python

Written by @ColeB2

class Solution:
    def cloneGraph(self, node: 'Node') -> 'Node':
        # Base case, return early
        if not node:
            return None
        # initialize our nodes hash map. This track whether we have
        # visited a node or node, as well as gives us access to the 
        # copies. Key: Value -> node.val, node copy.
        nodes = {node.val : Node(node.val)}
        # Stack/Queue containing node we are traversing and the copy.
        stack = [(node, nodes[node.val])]
        while stack:
            # pop off the node, and the copy
            n1, c1 = stack.pop()
            # traverse the node we popped, neighbors.
            for n in n1.neighbors:
                # Get our copy from our hash map, if it doesn't exist
                # we will create it based on the neighbors value.
                c2 = nodes.get(n.val, Node(n.val))
                # if neighbor hasn't been visited yet.
                if n.val not in nodes:
                    # add it to the stack to process later
                    stack.append((n, c2))
                    # add it to our visited hash map, with reference
                    # to the copy.
                    nodes[n.val] = c2
                # add the neighbor copies to our node copy.
                c1.neighbors.append(c2)
        # return the copy of our node. Above we created an undirected
        # graph, and the copies should all now point to the proper copies.
        return nodes[node.val]